Question Number 11203 by FilupS last updated on 16/Mar/17
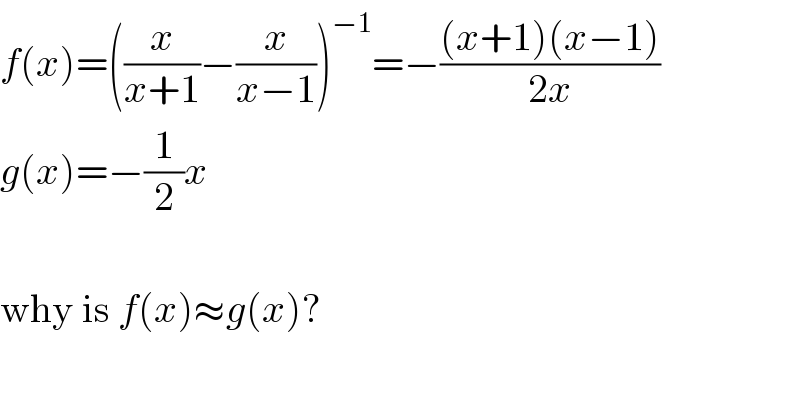
$${f}\left({x}\right)=\left(\frac{{x}}{{x}+\mathrm{1}}−\frac{{x}}{{x}−\mathrm{1}}\right)^{−\mathrm{1}} =−\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{\mathrm{2}{x}} \\ $$$${g}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{x} \\ $$$$\: \\ $$$$\mathrm{why}\:\mathrm{is}\:{f}\left({x}\right)\approx{g}\left({x}\right)? \\ $$
Answered by mrW1 last updated on 16/Mar/17
![f(x)=((x/(x+1))−(x/(x−1)))^(−1) =−(((x+1)(x−1))/(2x))=−((x^2 −1)/(2x))=−(x/2)+(1/(2x)) g(x)=−(x/2) f(x)−g(x)=(1/(2x)) lim_(x→∞) [f(x)−g(x)]=lim_(x→∞) (1/(2x))=0 it means with increasing ∣x∣, f(x)−g(x)→0 or f(x)≈g(x)](https://www.tinkutara.com/question/Q11205.png)
$${f}\left({x}\right)=\left(\frac{{x}}{{x}+\mathrm{1}}−\frac{{x}}{{x}−\mathrm{1}}\right)^{−\mathrm{1}} =−\frac{\left({x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)}{\mathrm{2}{x}}=−\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}=−\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{x}} \\ $$$${g}\left({x}\right)=−\frac{{x}}{\mathrm{2}} \\ $$$${f}\left({x}\right)−{g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}{x}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[{f}\left({x}\right)−{g}\left({x}\right)\right]=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{2}{x}}=\mathrm{0} \\ $$$${it}\:{means}\:{with}\:{increasing}\:\mid{x}\mid,\:{f}\left({x}\right)−{g}\left({x}\right)\rightarrow\mathrm{0} \\ $$$${or}\:{f}\left({x}\right)\approx{g}\left({x}\right) \\ $$
Commented by FilupS last updated on 17/Mar/17
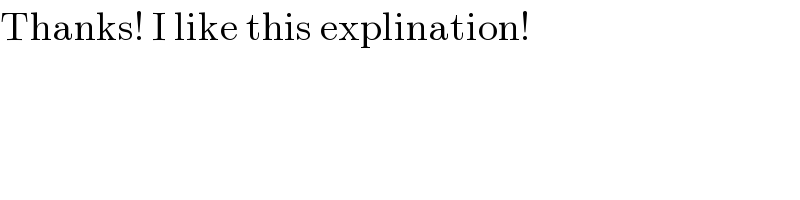
$$\mathrm{Thanks}!\:\mathrm{I}\:\mathrm{like}\:\mathrm{this}\:\mathrm{explination}! \\ $$
