Question Number 142285 by qaz last updated on 29/May/21
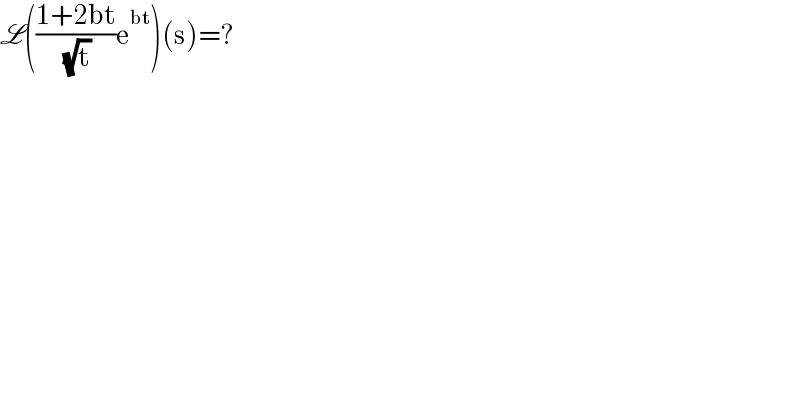
$$\mathscr{L}\left(\frac{\mathrm{1}+\mathrm{2bt}}{\:\sqrt{\mathrm{t}}}\mathrm{e}^{\mathrm{bt}} \right)\left(\mathrm{s}\right)=? \\ $$
Answered by Dwaipayan Shikari last updated on 29/May/21
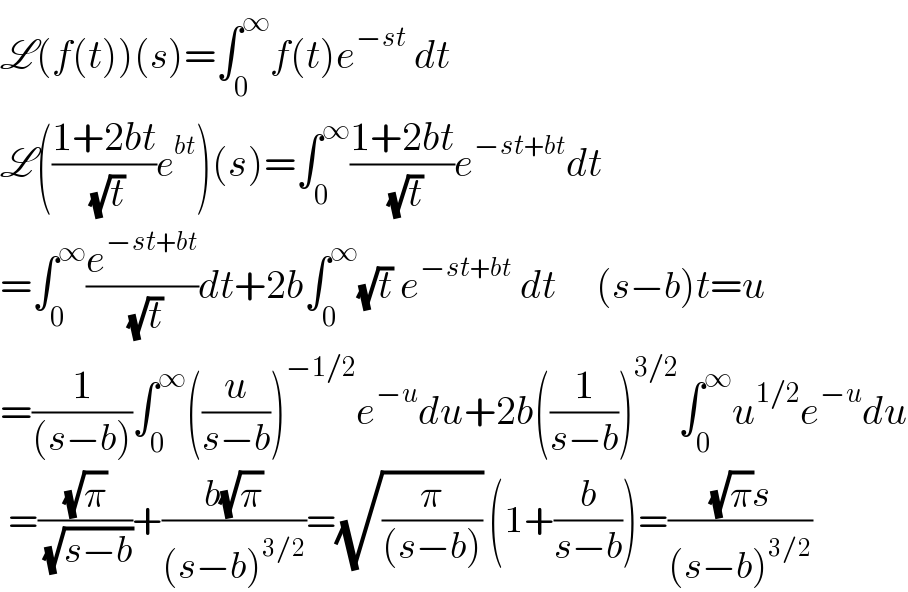
$$\mathscr{L}\left({f}\left({t}\right)\right)\left({s}\right)=\int_{\mathrm{0}} ^{\infty} {f}\left({t}\right){e}^{−{st}} \:{dt} \\ $$$$\mathscr{L}\left(\frac{\mathrm{1}+\mathrm{2}{bt}}{\:\sqrt{{t}}}{e}^{{bt}} \right)\left({s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\mathrm{2}{bt}}{\:\sqrt{{t}}}{e}^{−{st}+{bt}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{st}+{bt}} }{\:\sqrt{{t}}}{dt}+\mathrm{2}{b}\int_{\mathrm{0}} ^{\infty} \sqrt{{t}}\:{e}^{−{st}+{bt}} \:{dt}\:\:\:\:\:\left({s}−{b}\right){t}={u} \\ $$$$=\frac{\mathrm{1}}{\left({s}−{b}\right)}\int_{\mathrm{0}} ^{\infty} \left(\frac{{u}}{{s}−{b}}\right)^{−\mathrm{1}/\mathrm{2}} {e}^{−{u}} {du}+\mathrm{2}{b}\left(\frac{\mathrm{1}}{{s}−{b}}\right)^{\mathrm{3}/\mathrm{2}} \int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{1}/\mathrm{2}} {e}^{−{u}} {du} \\ $$$$\:=\frac{\sqrt{\pi}}{\:\sqrt{{s}−{b}}}+\frac{{b}\sqrt{\pi}}{\left({s}−{b}\right)^{\mathrm{3}/\mathrm{2}} }=\sqrt{\frac{\pi}{\left({s}−{b}\right)}}\:\left(\mathrm{1}+\frac{{b}}{{s}−{b}}\right)=\frac{\sqrt{\pi}{s}}{\left({s}−{b}\right)^{\mathrm{3}/\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 29/May/21
![L(((1+2bx)/( (√x)))e^(bx) )(s)=∫_0 ^∞ ((1+2bx)/( (√x)))e^(bx) e^(−sx) dx =∫_0 ^∞ ((1+2bx)/( (√x)))e^(−(s−b)x) dx =_((√x)=t) ∫_0 ^∞ ((1+2bt^2 )/t)e^(−(s−b)t^2 ) (2t)dt =2∫_0 ^∞ (1+2bt^2 )e^(−(s−b)t^2 ) dt =2∫_0 ^∞ e^(−(s−b)t^2 ) dt+4b∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt we have ∫_0 ^∞ e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(s−b))))=(1/( (√(s−b)))).((√π)/2) =((√π)/(2(√(s−b)))) ∫_0 ^∞ t^2 e^(−(s−b)t^2 ) dt =_((√(s−b))t=z) ∫_0 ^∞ (z^2 /(s−b))e^(−z^2 ) (dz/( (√(s−b))))=(1/((s−b)^(3/2) ))∫_0 ^∞ z^2 e^(−z^2 ) dz by parts ∫_0 ^∞ z^2 e^(−z^2 ) dz =−(1/2)∫_0 ^∞ z(−2z)e^(−z^2 ) dz =−(1/2){[ze^(−z^2 ) ]_0 ^∞ −∫_0 ^∞ e^(−z^2 ) dz} =(1/2).((√π)/2)=((√π)/4) ⇒ L(((1+2bx)/( (√x)))e^(bx) ) =((√π)/( (√(s−b))))+4b.(1/((s−b)^(3/2) )).((√π)/4) =((√π)/( (√(s−b))))+((b(√π))/((s−b)^(3/2) ))](https://www.tinkutara.com/question/Q142293.png)
$$\mathrm{L}\left(\frac{\mathrm{1}+\mathrm{2bx}}{\:\sqrt{\mathrm{x}}}\mathrm{e}^{\mathrm{bx}} \right)\left(\mathrm{s}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{2bx}}{\:\sqrt{\mathrm{x}}}\mathrm{e}^{\mathrm{bx}} \:\mathrm{e}^{−\mathrm{sx}} \:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{2bx}}{\:\sqrt{\mathrm{x}}}\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{x}} \:\mathrm{dx}\:=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{2bt}^{\mathrm{2}} }{\mathrm{t}}\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \left(\mathrm{1}+\mathrm{2bt}^{\mathrm{2}} \right)\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt}+\mathrm{4b}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{have}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=_{\sqrt{\mathrm{s}−\mathrm{b}}\mathrm{t}=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\:\sqrt{\mathrm{s}−\mathrm{b}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{s}−\mathrm{b}}}.\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{s}−\mathrm{b}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\left(\mathrm{s}−\mathrm{b}\right)\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:=_{\sqrt{\mathrm{s}−\mathrm{b}}\mathrm{t}=\mathrm{z}} \:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{z}^{\mathrm{2}} }{\mathrm{s}−\mathrm{b}}\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \frac{\mathrm{dz}}{\:\sqrt{\mathrm{s}−\mathrm{b}}}=\frac{\mathrm{1}}{\left(\mathrm{s}−\mathrm{b}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{z}\left(−\mathrm{2z}\right)\mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\left[\mathrm{ze}^{−\mathrm{z}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} −\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{z}^{\mathrm{2}} } \mathrm{dz}\right\}\:=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\sqrt{\pi}}{\mathrm{2}}=\frac{\sqrt{\pi}}{\mathrm{4}}\:\Rightarrow \\ $$$$\mathrm{L}\left(\frac{\mathrm{1}+\mathrm{2bx}}{\:\sqrt{\mathrm{x}}}\mathrm{e}^{\mathrm{bx}} \right)\:=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{s}−\mathrm{b}}}+\mathrm{4b}.\frac{\mathrm{1}}{\left(\mathrm{s}−\mathrm{b}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }.\frac{\sqrt{\pi}}{\mathrm{4}} \\ $$$$=\frac{\sqrt{\pi}}{\:\sqrt{\mathrm{s}−\mathrm{b}}}+\frac{\mathrm{b}\sqrt{\pi}}{\left(\mathrm{s}−\mathrm{b}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$
