Question Number 142325 by loveineq last updated on 30/May/21
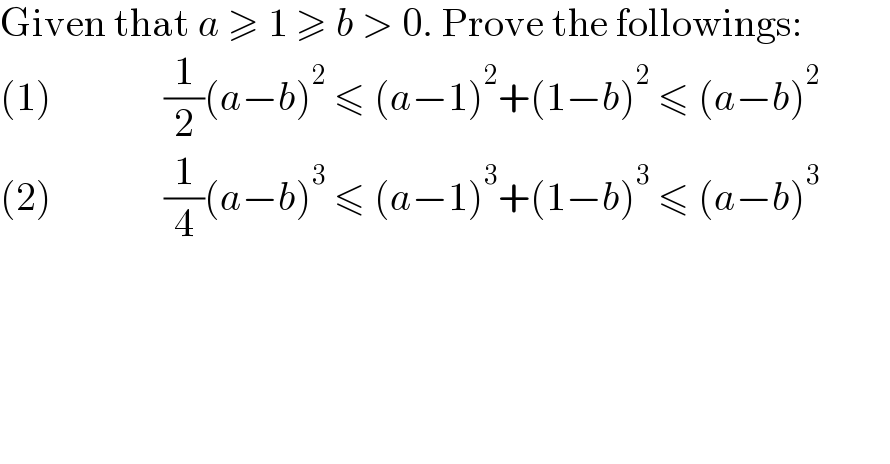
$$\mathrm{Given}\:\mathrm{that}\:{a}\:\geqslant\:\mathrm{1}\:\geqslant\:{b}\:>\:\mathrm{0}.\:\mathrm{Prove}\:\mathrm{the}\:\mathrm{followings}:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\left({a}−{b}\right)^{\mathrm{2}} \:\leqslant\:\left({a}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{1}−{b}\right)^{\mathrm{2}} \:\leqslant\:\left({a}−{b}\right)^{\mathrm{2}} \:\:\:\: \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({a}−{b}\right)^{\mathrm{3}} \:\leqslant\:\left({a}−\mathrm{1}\right)^{\mathrm{3}} +\left(\mathrm{1}−{b}\right)^{\mathrm{3}} \:\leqslant\:\left({a}−{b}\right)^{\mathrm{3}} \\ $$$$ \\ $$
