Question Number 76812 by Rio Michael last updated on 30/Dec/19
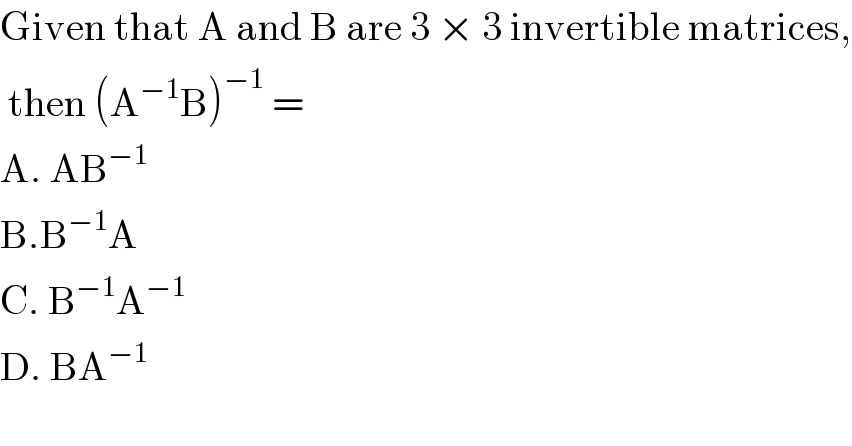
$$\mathrm{Given}\:\mathrm{that}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{3}\:×\:\mathrm{3}\:\mathrm{invertible}\:\mathrm{matrices}, \\ $$$$\:\mathrm{then}\:\left(\mathrm{A}^{−\mathrm{1}} \mathrm{B}\right)^{−\mathrm{1}} \:= \\ $$$$\mathrm{A}.\:\mathrm{AB}^{−\mathrm{1}} \\ $$$$\mathrm{B}.\mathrm{B}^{−\mathrm{1}} \mathrm{A} \\ $$$$\mathrm{C}.\:\mathrm{B}^{−\mathrm{1}} \mathrm{A}^{−\mathrm{1}} \\ $$$$\mathrm{D}.\:\mathrm{BA}^{−\mathrm{1}} \\ $$
Answered by benjo 1/2 santuyy last updated on 30/Dec/19

$${B}^{−\mathrm{1}} \:{A} \\ $$
