Menu Close

Given-2-cos-A-cos-B-cos-3-B-2-sin-A-sin-B-sin-3-B-what-is-the-value-of-sin-A-B-

Tinku Tara 0 Comments
Pin




Question Number 132006 by bramlexs22 last updated on 10/Feb/21
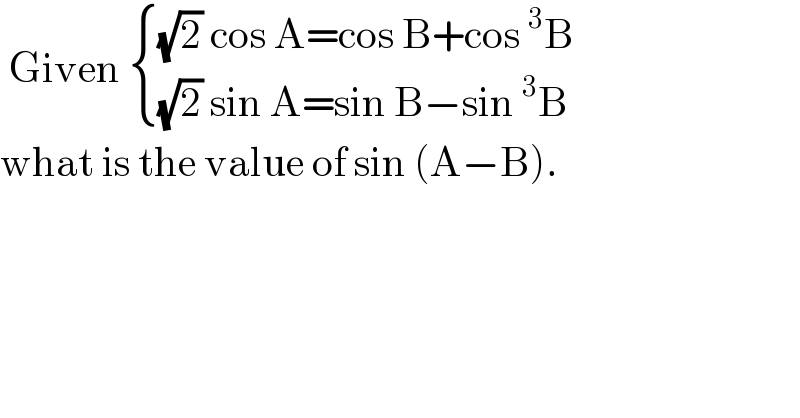
Given { (((√2) cos A=cos B+cos^3 B)),(((√2) sin A=sin B−sin^3 B)) :} what is the value of sin (A−B).
$$\:\mathrm{Given}\:\begin{cases}{\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{A}=\mathrm{cos}\:\mathrm{B}+\mathrm{cos}\:^{\mathrm{3}} \mathrm{B}}\\{\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{A}=\mathrm{sin}\:\mathrm{B}−\mathrm{sin}\:^{\mathrm{3}} \mathrm{B}}\end{cases} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\left(\mathrm{A}−\mathrm{B}\right). \\ $$
Answered by EDWIN88 last updated on 10/Feb/21
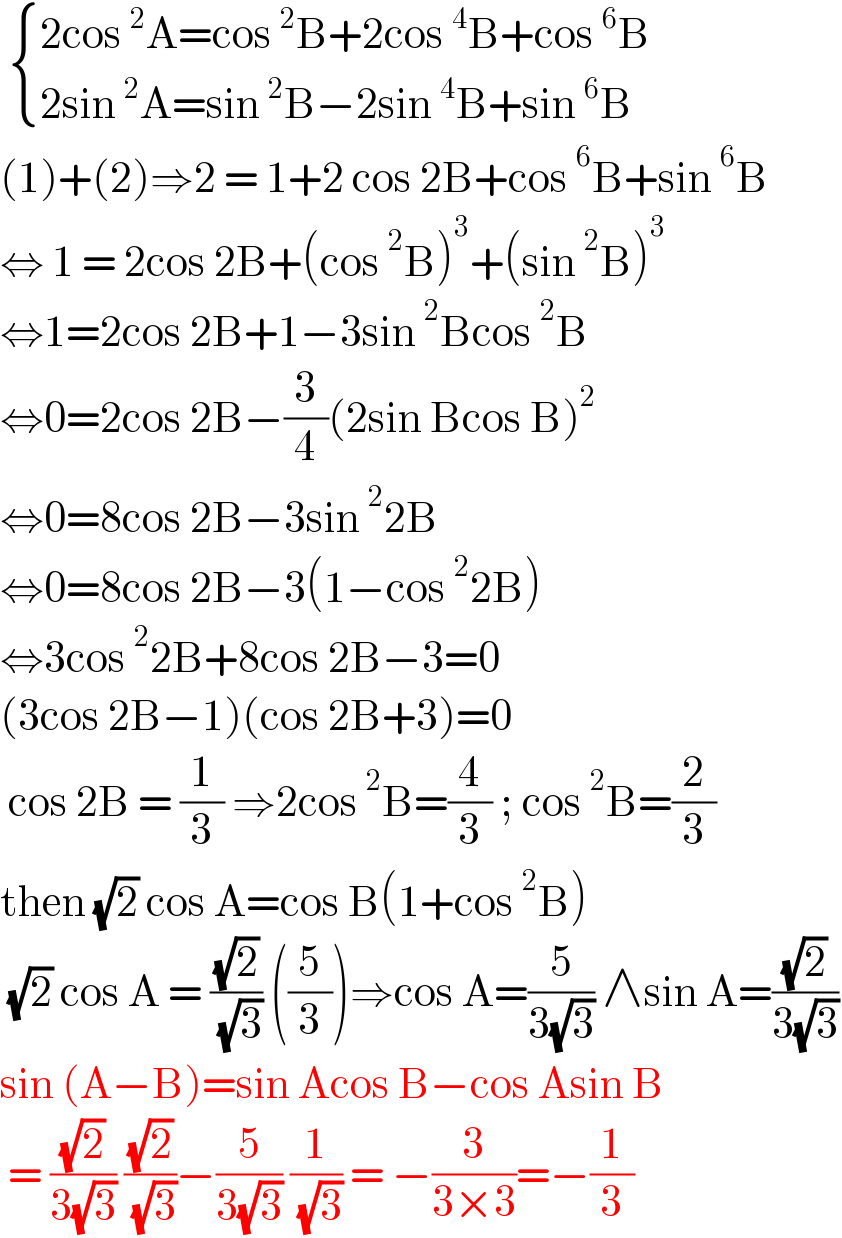
{ ((2cos^2 A=cos^2 B+2cos^4 B+cos^6 B)),((2sin^2 A=sin^2 B−2sin^4 B+sin^6 B)) :} (1)+(2)⇒2 = 1+2 cos 2B+cos^6 B+sin^6 B ⇔ 1 = 2cos 2B+(cos^2 B)^3 +(sin^2 B)^3 ⇔1=2cos 2B+1−3sin^2 Bcos^2 B ⇔0=2cos 2B−(3/4)(2sin Bcos B)^2 ⇔0=8cos 2B−3sin^2 2B ⇔0=8cos 2B−3(1−cos^2 2B) ⇔3cos^2 2B+8cos 2B−3=0 (3cos 2B−1)(cos 2B+3)=0 cos 2B = (1/3) ⇒2cos^2 B=(4/3) ; cos^2 B=(2/3) then (√2) cos A=cos B(1+cos^2 B) (√2) cos A = ((√2)/( (√3))) ((5/3))⇒cos A=(5/(3(√3))) ∧sin A=((√2)/(3(√3))) sin (A−B)=sin Acos B−cos Asin B = ((√2)/(3(√3))) ((√2)/( (√3)))−(5/(3(√3))) (1/( (√3))) = −(3/(3×3))=−(1/3)
$$\:\begin{cases}{\mathrm{2cos}\:^{\mathrm{2}} \mathrm{A}=\mathrm{cos}\:^{\mathrm{2}} \mathrm{B}+\mathrm{2cos}\:^{\mathrm{4}} \mathrm{B}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{B}}\\{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{A}=\mathrm{sin}\:^{\mathrm{2}} \mathrm{B}−\mathrm{2sin}\:^{\mathrm{4}} \mathrm{B}+\mathrm{sin}\:^{\mathrm{6}} \mathrm{B}}\end{cases} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow\mathrm{2}\:=\:\mathrm{1}+\mathrm{2}\:\mathrm{cos}\:\mathrm{2B}+\mathrm{cos}\:^{\mathrm{6}} \mathrm{B}+\mathrm{sin}\:^{\mathrm{6}} \mathrm{B} \\ $$$$\Leftrightarrow\:\mathrm{1}\:=\:\mathrm{2cos}\:\mathrm{2B}+\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{B}\right)^{\mathrm{3}} +\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{B}\right)^{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{1}=\mathrm{2cos}\:\mathrm{2B}+\mathrm{1}−\mathrm{3sin}\:^{\mathrm{2}} \mathrm{Bcos}\:^{\mathrm{2}} \mathrm{B} \\ $$$$\Leftrightarrow\mathrm{0}=\mathrm{2cos}\:\mathrm{2B}−\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2sin}\:\mathrm{Bcos}\:\mathrm{B}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{0}=\mathrm{8cos}\:\mathrm{2B}−\mathrm{3sin}\:^{\mathrm{2}} \mathrm{2B} \\ $$$$\Leftrightarrow\mathrm{0}=\mathrm{8cos}\:\mathrm{2B}−\mathrm{3}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{2B}\right) \\ $$$$\Leftrightarrow\mathrm{3cos}\:^{\mathrm{2}} \mathrm{2B}+\mathrm{8cos}\:\mathrm{2B}−\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{3cos}\:\mathrm{2B}−\mathrm{1}\right)\left(\mathrm{cos}\:\mathrm{2B}+\mathrm{3}\right)=\mathrm{0} \\ $$$$\:\mathrm{cos}\:\mathrm{2B}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{2cos}\:^{\mathrm{2}} \mathrm{B}=\frac{\mathrm{4}}{\mathrm{3}}\:;\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{B}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\mathrm{then}\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{A}=\mathrm{cos}\:\mathrm{B}\left(\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{B}\right)\: \\ $$$$\:\sqrt{\mathrm{2}}\:\mathrm{cos}\:\mathrm{A}\:=\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\:\left(\frac{\mathrm{5}}{\mathrm{3}}\right)\Rightarrow\mathrm{cos}\:\mathrm{A}=\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\wedge\mathrm{sin}\:\mathrm{A}=\frac{\sqrt{\mathrm{2}}}{\mathrm{3}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{sin}\:\left(\mathrm{A}−\mathrm{B}\right)=\mathrm{sin}\:\mathrm{Acos}\:\mathrm{B}−\mathrm{cos}\:\mathrm{Asin}\:\mathrm{B} \\ $$$$\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{5}}{\mathrm{3}\sqrt{\mathrm{3}}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:=\:−\frac{\mathrm{3}}{\mathrm{3}×\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *