Question Number 142437 by mohammad17 last updated on 31/May/21

Answered by Dwaipayan Shikari last updated on 31/May/21
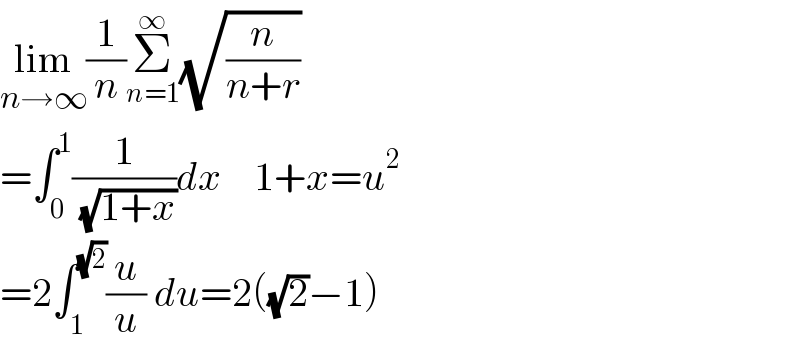
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\sqrt{\frac{{n}}{{n}+{r}}}\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}{dx}\:\:\:\:\mathrm{1}+{x}={u}^{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \frac{{u}}{{u}}\:{du}=\mathrm{2}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$
