Question Number 76929 by peter frank last updated on 01/Jan/20
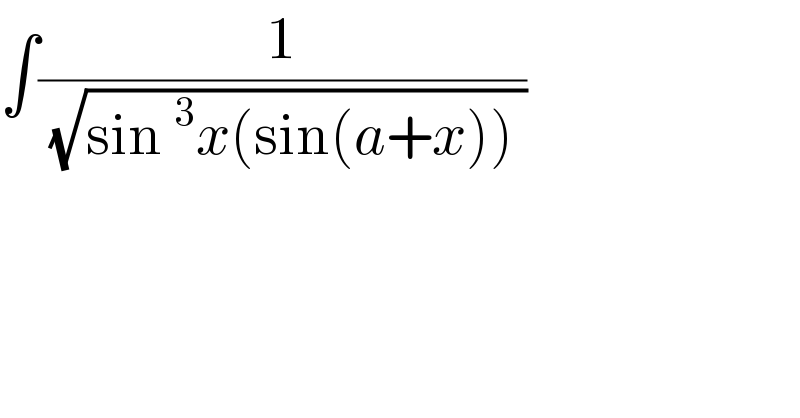
$$\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{sin}\:^{\mathrm{3}} {x}\left(\mathrm{sin}\left({a}+{x}\right)\right)\:}} \\ $$
Answered by MJS last updated on 01/Jan/20
![∫(dx/( (√(sin^3 x sin (a+x)))))= =∫(dx/( (√(sin^3 x (sin a cos x +cos a sin x)))))= [sin a =q; cos a =p] =∫(dx/( (√(psin^4 x +q cos x sin^3 x))))= [t=tan x → dx=cos^2 x dt=(dt/(t^2 +1))] =∫(dt/( (√(t^3 (pt+q)))))= [u=(√(pt+q)) → dt=((2(√(pt+q)))/p)] =2(√p)∫(du/((u^2 −q)^(3/2) ))=−((2(√p))/q)×(u/( (√(u^2 −p))))= =−(2/q)(√(p+(q/t)))=−(2/q)(√(p+qcot x))= =−(2/(sin a))(√(cos a +sin a cot x))+C](https://www.tinkutara.com/question/Q76942.png)
$$\int\frac{{dx}}{\:\sqrt{\mathrm{sin}^{\mathrm{3}} \:{x}\:\mathrm{sin}\:\left({a}+{x}\right)}}= \\ $$$$=\int\frac{{dx}}{\:\sqrt{\mathrm{sin}^{\mathrm{3}} \:{x}\:\left(\mathrm{sin}\:{a}\:\mathrm{cos}\:{x}\:+\mathrm{cos}\:{a}\:\mathrm{sin}\:{x}\right)}}= \\ $$$$\:\:\:\:\:\left[\mathrm{sin}\:{a}\:={q};\:\mathrm{cos}\:{a}\:={p}\right] \\ $$$$=\int\frac{{dx}}{\:\sqrt{{p}\mathrm{sin}^{\mathrm{4}} \:{x}\:+{q}\:\mathrm{cos}\:{x}\:\mathrm{sin}^{\mathrm{3}} \:{x}}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{dt}}{\:\sqrt{{t}^{\mathrm{3}} \left({pt}+{q}\right)}}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{{pt}+{q}}\:\rightarrow\:{dt}=\frac{\mathrm{2}\sqrt{{pt}+{q}}}{{p}}\right] \\ $$$$=\mathrm{2}\sqrt{{p}}\int\frac{{du}}{\left({u}^{\mathrm{2}} −{q}\right)^{\mathrm{3}/\mathrm{2}} }=−\frac{\mathrm{2}\sqrt{{p}}}{{q}}×\frac{{u}}{\:\sqrt{{u}^{\mathrm{2}} −{p}}}= \\ $$$$=−\frac{\mathrm{2}}{{q}}\sqrt{{p}+\frac{{q}}{{t}}}=−\frac{\mathrm{2}}{{q}}\sqrt{{p}+{q}\mathrm{cot}\:{x}}= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{sin}\:{a}}\sqrt{\mathrm{cos}\:{a}\:+\mathrm{sin}\:{a}\:\mathrm{cot}\:{x}}+{C} \\ $$
Commented by peter frank last updated on 01/Jan/20

$${thank}\:{you} \\ $$
Answered by petrochengula last updated on 03/Jan/20

$$=\int\frac{\mathrm{1}}{\:\sqrt{\frac{{sin}^{\mathrm{4}} {x}\left({sinacosx}+{sinxcosa}\right.}{{sinx}}}} \\ $$$$=\int\frac{\mathrm{1}}{{sin}^{\mathrm{2}} {x}\sqrt{{sinacotx}+{cosa}}}{dx} \\ $$$$=\int\frac{{cosec}^{\mathrm{2}} {x}}{\:\sqrt{{sinacotx}+{cosa}}}{dx} \\ $$$$=−\int\frac{−{cosec}^{\mathrm{2}} {x}}{\:\sqrt{{sinacotx}+{cosa}}}{dx} \\ $$$${let}\:{t}=\sqrt{{sinacotx}+{cosa}} \\ $$$${game}\:{over} \\ $$
