Question Number 11459 by @ANTARES_VY last updated on 26/Mar/17
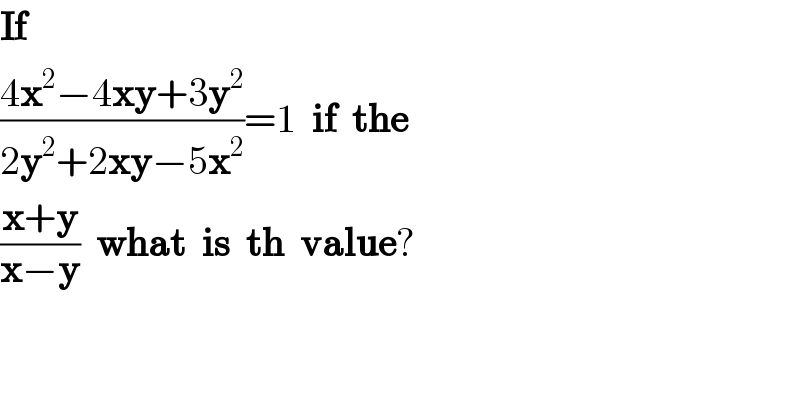
$$\boldsymbol{\mathrm{If}} \\ $$$$\frac{\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{4}\boldsymbol{\mathrm{xy}}+\mathrm{3}\boldsymbol{\mathrm{y}}^{\mathrm{2}} }{\mathrm{2}\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{xy}}−\mathrm{5}\boldsymbol{\mathrm{x}}^{\mathrm{2}} }=\mathrm{1}\:\:\boldsymbol{\mathrm{if}}\:\:\boldsymbol{\mathrm{the}} \\ $$$$\frac{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}}\:\:\boldsymbol{\mathrm{what}}\:\:\boldsymbol{\mathrm{is}}\:\:\boldsymbol{\mathrm{th}}\:\:\boldsymbol{\mathrm{value}}? \\ $$
Answered by ajfour last updated on 26/Mar/17

$$−\mathrm{2} \\ $$
Commented by ajfour last updated on 26/Mar/17
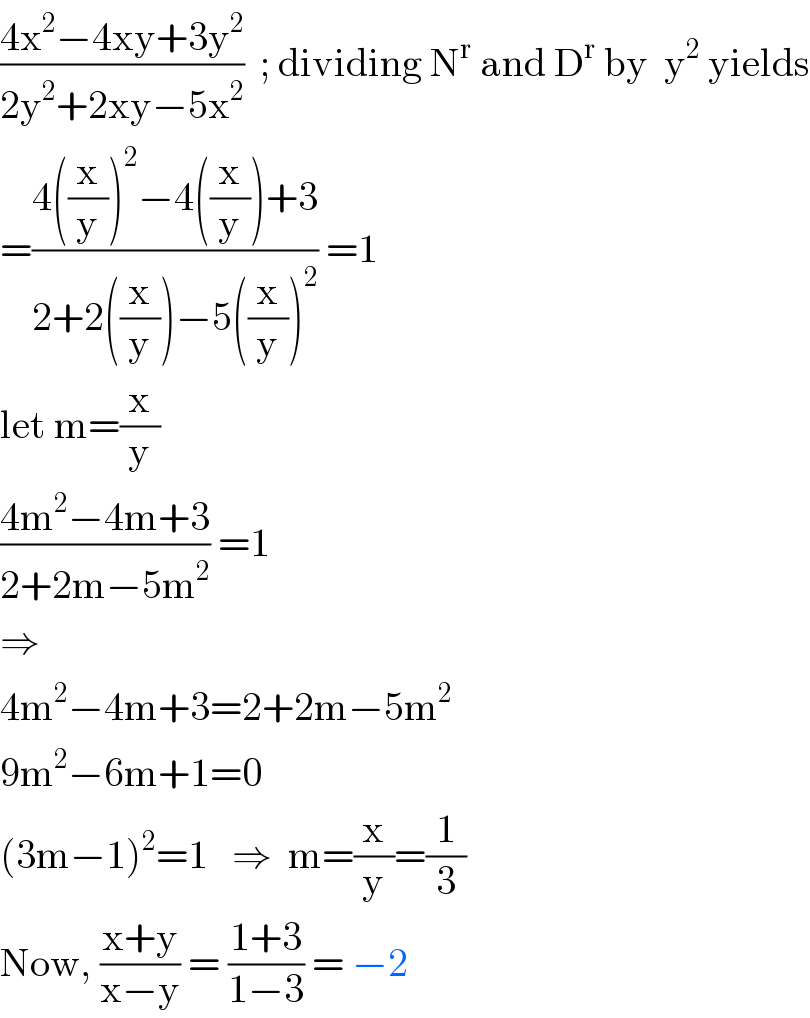
$$\frac{\mathrm{4x}^{\mathrm{2}} −\mathrm{4xy}+\mathrm{3y}^{\mathrm{2}} }{\mathrm{2y}^{\mathrm{2}} +\mathrm{2xy}−\mathrm{5x}^{\mathrm{2}} }\:\:;\:\mathrm{dividing}\:\mathrm{N}^{\mathrm{r}} \:\mathrm{and}\:\mathrm{D}^{\mathrm{r}} \:\mathrm{by}\:\:\mathrm{y}^{\mathrm{2}} \:\mathrm{yields} \\ $$$$=\frac{\mathrm{4}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)^{\mathrm{2}} −\mathrm{4}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)+\mathrm{3}}{\mathrm{2}+\mathrm{2}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)−\mathrm{5}\left(\frac{\mathrm{x}}{\mathrm{y}}\right)^{\mathrm{2}} }\:=\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{m}=\frac{\mathrm{x}}{\mathrm{y}} \\ $$$$\frac{\mathrm{4m}^{\mathrm{2}} −\mathrm{4m}+\mathrm{3}}{\mathrm{2}+\mathrm{2m}−\mathrm{5m}^{\mathrm{2}} }\:=\mathrm{1} \\ $$$$\Rightarrow\: \\ $$$$\mathrm{4m}^{\mathrm{2}} −\mathrm{4m}+\mathrm{3}=\mathrm{2}+\mathrm{2m}−\mathrm{5m}^{\mathrm{2}} \\ $$$$\mathrm{9m}^{\mathrm{2}} −\mathrm{6m}+\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{3m}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1}\:\:\:\Rightarrow\:\:\mathrm{m}=\frac{\mathrm{x}}{\mathrm{y}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{Now},\:\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}\:=\:\frac{\mathrm{1}+\mathrm{3}}{\mathrm{1}−\mathrm{3}}\:=\:−\mathrm{2} \\ $$
Answered by ridwan balatif last updated on 26/Mar/17
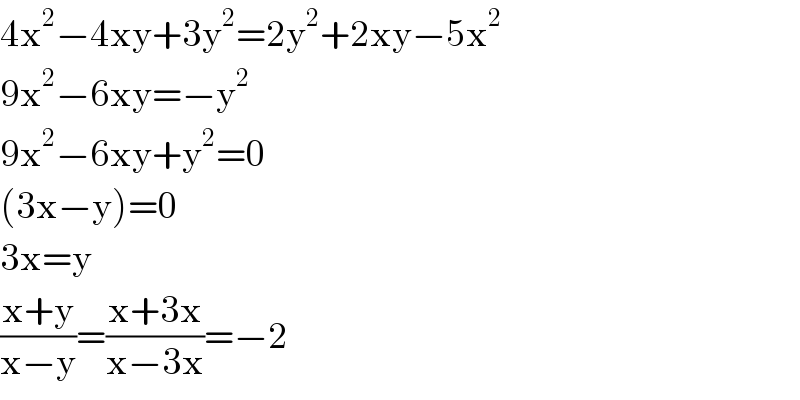
$$\mathrm{4x}^{\mathrm{2}} −\mathrm{4xy}+\mathrm{3y}^{\mathrm{2}} =\mathrm{2y}^{\mathrm{2}} +\mathrm{2xy}−\mathrm{5x}^{\mathrm{2}} \\ $$$$\mathrm{9x}^{\mathrm{2}} −\mathrm{6xy}=−\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{9x}^{\mathrm{2}} −\mathrm{6xy}+\mathrm{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left(\mathrm{3x}−\mathrm{y}\right)=\mathrm{0} \\ $$$$\mathrm{3x}=\mathrm{y} \\ $$$$\frac{\mathrm{x}+\mathrm{y}}{\mathrm{x}−\mathrm{y}}=\frac{\mathrm{x}+\mathrm{3x}}{\mathrm{x}−\mathrm{3x}}=−\mathrm{2} \\ $$
Commented by @ANTARES_VY last updated on 26/Mar/17

$$\mathbb{THENKS} \\ $$
Commented by @ANTARES_VY last updated on 26/Mar/17

$$\mathbb{THENKS} \\ $$
