Menu Close

One-vertex-of-the-equalateral-triangle-with-centroid-at-the-origin-and-one-side-as-x-y-2-0-is-a-1-1-b-2-2-c-2-2-d-2-2-

Tinku Tara 0 Comments
Pin




Question Number 77000 by vishalbhardwaj last updated on 02/Jan/20
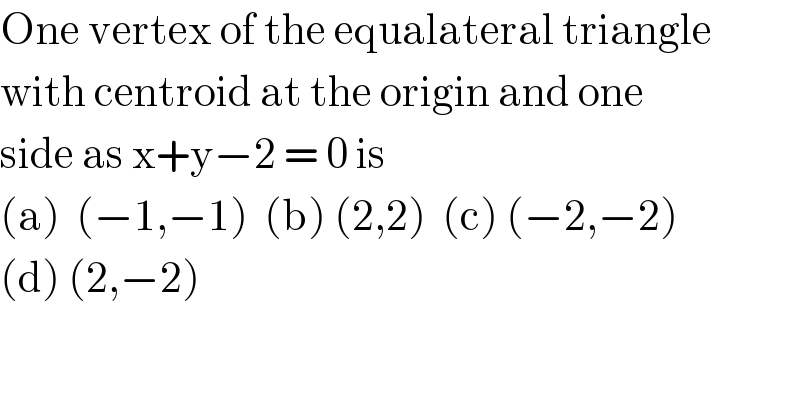
One vertex of the equalateral triangle with centroid at the origin and one side as x+y−2 = 0 is (a) (−1,−1) (b) (2,2) (c) (−2,−2) (d) (2,−2)
$$\mathrm{One}\:\mathrm{vertex}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equalateral}\:\mathrm{triangle} \\ $$$$\mathrm{with}\:\mathrm{centroid}\:\mathrm{at}\:\mathrm{the}\:\mathrm{origin}\:\mathrm{and}\:\mathrm{one} \\ $$$$\mathrm{side}\:\mathrm{as}\:\mathrm{x}+\mathrm{y}−\mathrm{2}\:=\:\mathrm{0}\:\mathrm{is} \\ $$$$\left(\mathrm{a}\right)\:\:\left(−\mathrm{1},−\mathrm{1}\right)\:\:\left(\mathrm{b}\right)\:\left(\mathrm{2},\mathrm{2}\right)\:\:\left(\mathrm{c}\right)\:\left(−\mathrm{2},−\mathrm{2}\right) \\ $$$$\left(\mathrm{d}\right)\:\left(\mathrm{2},−\mathrm{2}\right) \\ $$
Commented by vishalbhardwaj last updated on 03/Jan/20
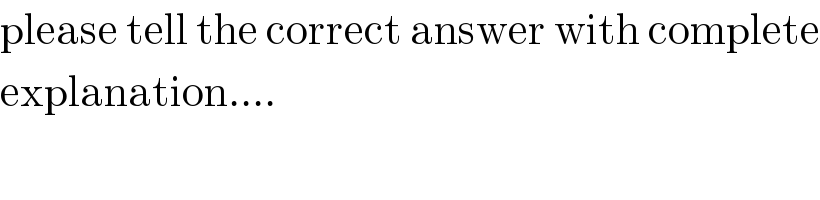
please tell the correct answer with complete explanation....
$$\mathrm{please}\:\mathrm{tell}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}\:\mathrm{with}\:\mathrm{complete} \\ $$$$\mathrm{explanation}…. \\ $$
Answered by mr W last updated on 04/Jan/20
distance from origin to given line: ((∣0×1+0×1−2∣)/( (√(1^2 +1^2 ))))=(√2) perpendicular line through origin: y=x the vertex must lie on this line, therefore (a),(b),(c) are possible. distance from vertex to the origin is 2 times of the distance from origin to the given line, i.e. 2(√2), therefore (b) and (c) are possible. distance from vertex to given line is 3 times of that from origin, i.e. 3(√2), (b): ((∣2×1+2×1−2∣)/( (√(1^2 +1^2 ))))=(√2)≠3(√2) (c): ((∣−2×1−2×1−2∣)/( (√(1^2 +1^2 ))))=3(√2) ⇒only (c) is correct.
$${distance}\:{from}\:{origin}\:{to}\:{given}\:{line}: \\ $$$$\frac{\mid\mathrm{0}×\mathrm{1}+\mathrm{0}×\mathrm{1}−\mathrm{2}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\sqrt{\mathrm{2}} \\ $$$${perpendicular}\:{line}\:{through}\:{origin}: \\ $$$${y}={x} \\ $$$${the}\:{vertex}\:{must}\:{lie}\:{on}\:{this}\:{line}, \\ $$$${therefore}\:\left({a}\right),\left({b}\right),\left({c}\right)\:{are}\:{possible}. \\ $$$${distance}\:{from}\:{vertex}\:{to}\:{the}\:{origin} \\ $$$${is}\:\mathrm{2}\:{times}\:{of}\:{the}\:{distance}\:{from}\:{origin} \\ $$$${to}\:{the}\:{given}\:{line},\:{i}.{e}.\:\mathrm{2}\sqrt{\mathrm{2}},\:{therefore} \\ $$$$\left({b}\right)\:{and}\:\left({c}\right)\:{are}\:{possible}. \\ $$$${distance}\:{from}\:{vertex}\:{to}\:{given}\:{line} \\ $$$${is}\:\mathrm{3}\:{times}\:{of}\:{that}\:{from}\:{origin}, \\ $$$${i}.{e}.\:\mathrm{3}\sqrt{\mathrm{2}}, \\ $$$$\left({b}\right):\:\frac{\mid\mathrm{2}×\mathrm{1}+\mathrm{2}×\mathrm{1}−\mathrm{2}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\sqrt{\mathrm{2}}\neq\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\left({c}\right):\:\frac{\mid−\mathrm{2}×\mathrm{1}−\mathrm{2}×\mathrm{1}−\mathrm{2}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow{only}\:\left({c}\right)\:{is}\:{correct}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *