Question Number 11547 by Nayon last updated on 28/Mar/17
![(d/dx)(x^x )=?[please give the answer with proof]](https://www.tinkutara.com/question/Q11547.png)
$$\:\:\:\:\:\:\:\:\:\:\frac{{d}}{{dx}}\left({x}^{{x}} \right)=?\left[{please}\:{give}\:{the}\:{answer}\:{with}\:{proof}\right] \\ $$
Answered by sma3l2996 last updated on 28/Mar/17
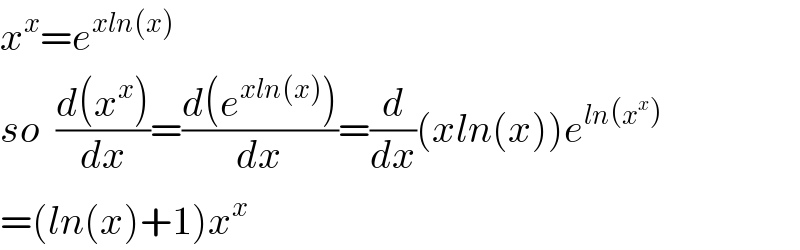
$${x}^{{x}} ={e}^{{xln}\left({x}\right)} \\ $$$${so}\:\:\frac{{d}\left({x}^{{x}} \right)}{{dx}}=\frac{{d}\left({e}^{{xln}\left({x}\right)} \right)}{{dx}}=\frac{{d}}{{dx}}\left({xln}\left({x}\right)\right){e}^{{ln}\left({x}^{{x}} \right)} \\ $$$$=\left({ln}\left({x}\right)+\mathrm{1}\right){x}^{{x}} \\ $$
Answered by ajfour last updated on 28/Mar/17
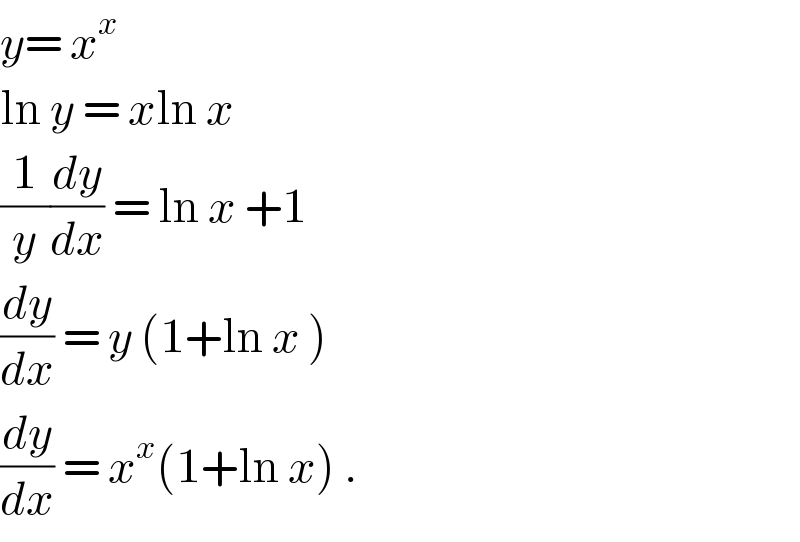
$${y}=\:{x}^{{x}} \\ $$$$\mathrm{ln}\:{y}\:=\:{x}\mathrm{ln}\:{x} \\ $$$$\frac{\mathrm{1}}{{y}}\frac{{dy}}{{dx}}\:=\:\mathrm{ln}\:{x}\:+\mathrm{1} \\ $$$$\frac{{dy}}{{dx}}\:=\:{y}\:\left(\mathrm{1}+\mathrm{ln}\:{x}\:\right) \\ $$$$\frac{{dy}}{{dx}}\:=\:{x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)\:. \\ $$
