Question Number 142630 by iloveisrael last updated on 03/Jun/21
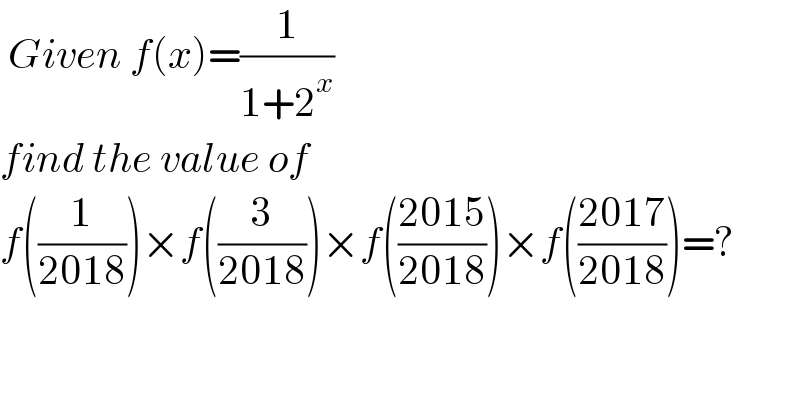
$$\:{Given}\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{{x}} } \\ $$$${find}\:{the}\:{value}\:{of} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{2018}}\right)×{f}\left(\frac{\mathrm{3}}{\mathrm{2018}}\right)×{f}\left(\frac{\mathrm{2015}}{\mathrm{2018}}\right)×{f}\left(\frac{\mathrm{2017}}{\mathrm{2018}}\right)=? \\ $$
Commented by MJS_new last updated on 03/Jun/21
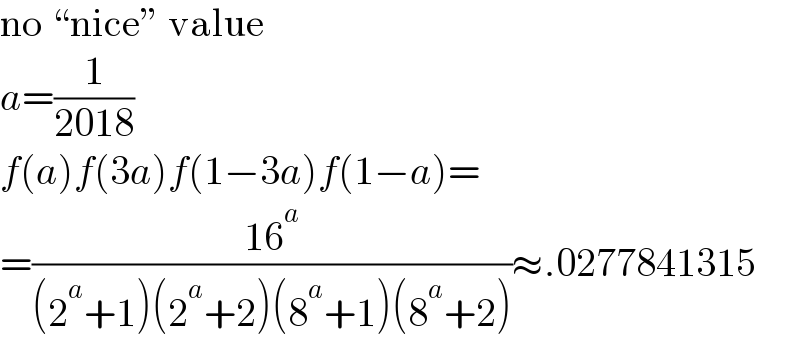
$$\mathrm{no}\:“\mathrm{nice}''\:\mathrm{value} \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{2018}} \\ $$$${f}\left({a}\right){f}\left(\mathrm{3}{a}\right){f}\left(\mathrm{1}−\mathrm{3}{a}\right){f}\left(\mathrm{1}−{a}\right)= \\ $$$$=\frac{\mathrm{16}^{{a}} }{\left(\mathrm{2}^{{a}} +\mathrm{1}\right)\left(\mathrm{2}^{{a}} +\mathrm{2}\right)\left(\mathrm{8}^{{a}} +\mathrm{1}\right)\left(\mathrm{8}^{{a}} +\mathrm{2}\right)}\approx.\mathrm{0277841315} \\ $$
