Question Number 142667 by mnjuly1970 last updated on 03/Jun/21
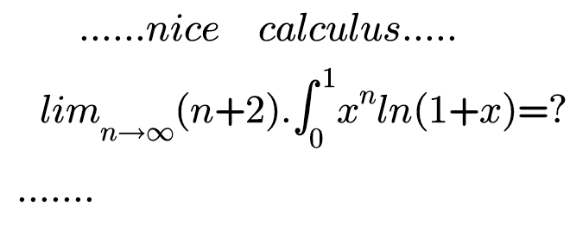
Answered by mindispower last updated on 03/Jun/21
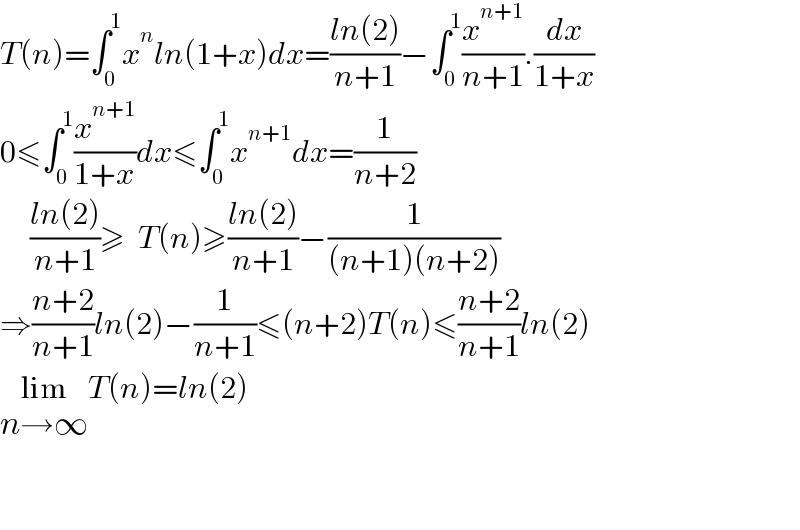
$${T}\left({n}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} {ln}\left(\mathrm{1}+{x}\right){dx}=\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}.\frac{{dx}}{\mathrm{1}+{x}} \\ $$$$\mathrm{0}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{\mathrm{1}+{x}}{dx}\leqslant\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}+\mathrm{1}} {dx}=\frac{\mathrm{1}}{{n}+\mathrm{2}} \\ $$$$\:\:\:\:\:\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}}\geqslant\:\:{T}\left({n}\right)\geqslant\frac{{ln}\left(\mathrm{2}\right)}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$\Rightarrow\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{{n}+\mathrm{1}}\leqslant\left({n}+\mathrm{2}\right){T}\left({n}\right)\leqslant\frac{{n}+\mathrm{2}}{{n}+\mathrm{1}}{ln}\left(\mathrm{2}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{T}\left({n}\right)={ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 03/Jun/21

$${thanks}\:{alot}…. \\ $$
