Question Number 11594 by JAZAR last updated on 28/Mar/17
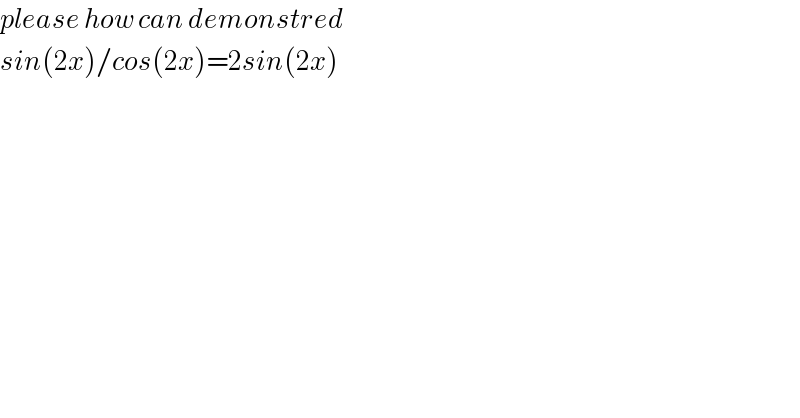
$${please}\:{how}\:{can}\:{demonstred}\: \\ $$$${sin}\left(\mathrm{2}{x}\underset{} {\right)}/{cos}\left(\mathrm{2}{x}\right)=\mathrm{2}{sin}\left(\mathrm{2}{x}\right) \\ $$
Answered by mrW1 last updated on 28/Mar/17
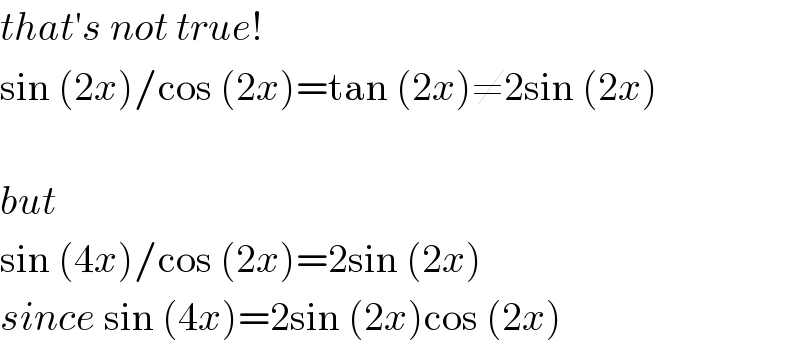
$${that}'{s}\:{not}\:{true}! \\ $$$$\mathrm{sin}\:\left(\mathrm{2}{x}\right)/\mathrm{cos}\:\left(\mathrm{2}{x}\right)=\mathrm{tan}\:\left(\mathrm{2}{x}\right)\neq\mathrm{2sin}\:\left(\mathrm{2}{x}\right) \\ $$$$ \\ $$$${but} \\ $$$$\mathrm{sin}\:\left(\mathrm{4}{x}\right)/\mathrm{cos}\:\left(\mathrm{2}{x}\right)=\mathrm{2sin}\:\left(\mathrm{2}{x}\right) \\ $$$${since}\:\mathrm{sin}\:\left(\mathrm{4}{x}\right)=\mathrm{2sin}\:\left(\mathrm{2}{x}\right)\mathrm{cos}\:\left(\mathrm{2}{x}\right) \\ $$
