Question Number 77131 by peter frank last updated on 03/Jan/20

Answered by mr W last updated on 03/Jan/20
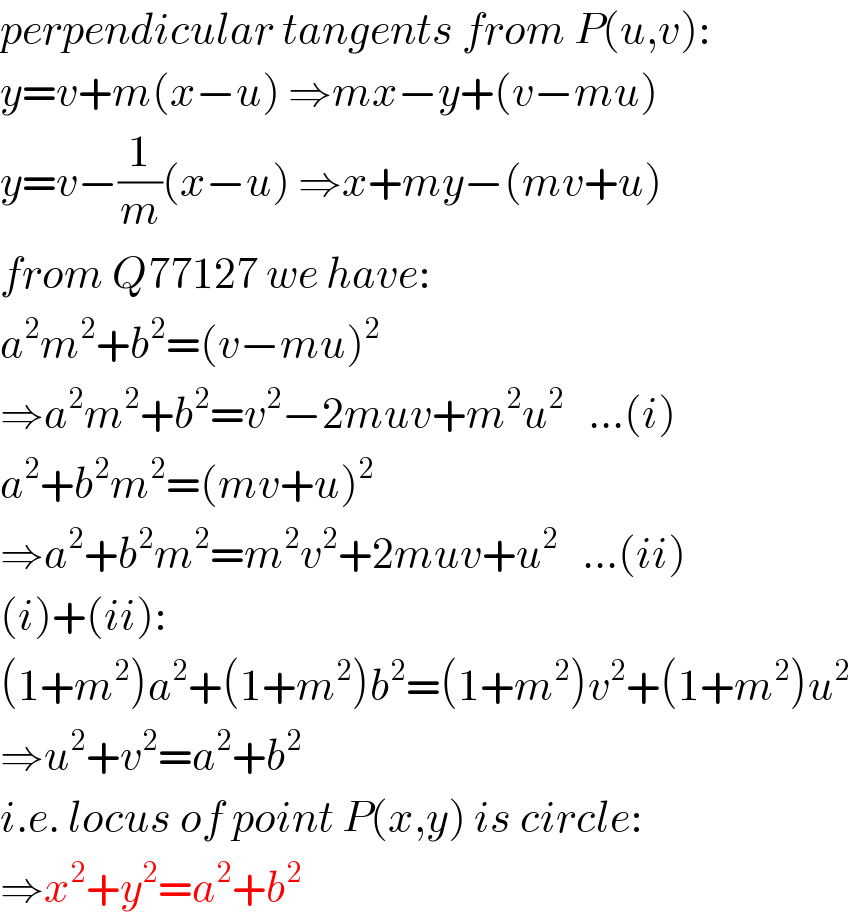
$${perpendicular}\:{tangents}\:{from}\:{P}\left({u},{v}\right): \\ $$$${y}={v}+{m}\left({x}−{u}\right)\:\Rightarrow{mx}−{y}+\left({v}−{mu}\right) \\ $$$${y}={v}−\frac{\mathrm{1}}{{m}}\left({x}−{u}\right)\:\Rightarrow{x}+{my}−\left({mv}+{u}\right) \\ $$$${from}\:{Q}\mathrm{77127}\:{we}\:{have}: \\ $$$${a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} =\left({v}−{mu}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {m}^{\mathrm{2}} +{b}^{\mathrm{2}} ={v}^{\mathrm{2}} −\mathrm{2}{muv}+{m}^{\mathrm{2}} {u}^{\mathrm{2}} \:\:\:…\left({i}\right) \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} =\left({mv}+{u}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{a}^{\mathrm{2}} +{b}^{\mathrm{2}} {m}^{\mathrm{2}} ={m}^{\mathrm{2}} {v}^{\mathrm{2}} +\mathrm{2}{muv}+{u}^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\left(\mathrm{1}+{m}^{\mathrm{2}} \right){a}^{\mathrm{2}} +\left(\mathrm{1}+{m}^{\mathrm{2}} \right){b}^{\mathrm{2}} =\left(\mathrm{1}+{m}^{\mathrm{2}} \right){v}^{\mathrm{2}} +\left(\mathrm{1}+{m}^{\mathrm{2}} \right){u}^{\mathrm{2}} \\ $$$$\Rightarrow{u}^{\mathrm{2}} +{v}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${i}.{e}.\:{locus}\:{of}\:{point}\:{P}\left({x},{y}\right)\:{is}\:{circle}: \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$
Commented by peter frank last updated on 06/Jan/20
$${thank}\:{for}\:{your}\:{help}.{I}\:{have} \\ $$$${learnt}\:{so}\:{much}\:{sir} \\ $$
