Question Number 11599 by tawa last updated on 28/Mar/17

$$\mathrm{A}\:\mathrm{number}\:\mathrm{is}\:\mathrm{selected}\:\mathrm{at}\:\mathrm{random}\:\mathrm{from}\:\mathrm{the}\:\mathrm{integers}\:\mathrm{10}\:\mathrm{to}\:\mathrm{35}\:\mathrm{exclussive},\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{chances}\:\mathrm{take}\:\mathrm{the}\:\mathrm{subsets}\:\mathrm{of}\:\mathrm{P},\:\mathrm{Q}\:\mathrm{and}\:\mathrm{R}\:\mathrm{respectively},\:\mathrm{where}\:\mathrm{P}\:\mathrm{is} \\ $$$$\mathrm{even}\:,\:\mathrm{Q}\:\mathrm{is}\:\mathrm{even}\:\mathrm{or}\:\mathrm{prime}\:\mathrm{number},\:\mathrm{and}\:\mathrm{R}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{prime}\:\mathrm{numbers}.\:\mathrm{What}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{probability}\: \\ $$$$\left(\mathrm{a}\right)\:\mathrm{That}\:\mathrm{exacly}\:\mathrm{one}\:\mathrm{of}\:\mathrm{the}\:\mathrm{events}\:\mathrm{of}\:\mathrm{the}\:\mathrm{subset}\:\mathrm{is}\:\mathrm{choosen}\:? \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Of}\:\mathrm{choosen}\:\mathrm{at}\:\mathrm{most}\:\mathrm{two}\:\mathrm{of}\:\mathrm{the}\:\mathrm{subset}\:\mathrm{of}\:\mathrm{the}\:\mathrm{event}. \\ $$
Answered by mrW1 last updated on 29/Mar/17
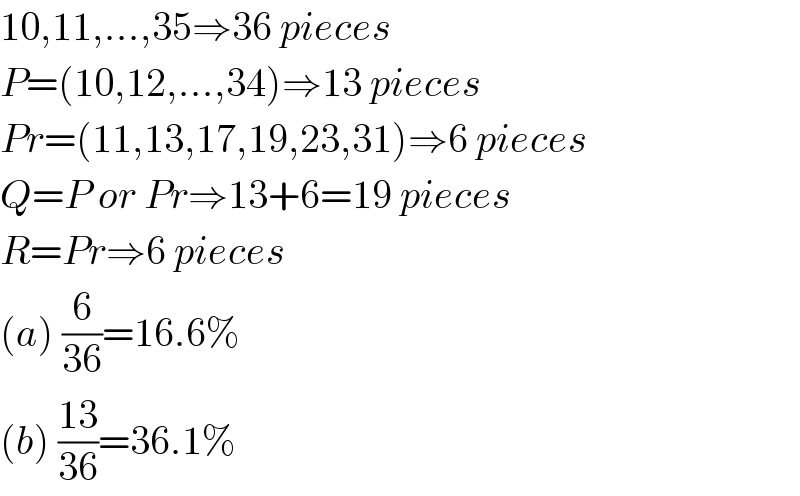
$$\mathrm{10},\mathrm{11},…,\mathrm{35}\Rightarrow\mathrm{36}\:{pieces} \\ $$$${P}=\left(\mathrm{10},\mathrm{12},…,\mathrm{34}\right)\Rightarrow\mathrm{13}\:{pieces} \\ $$$${Pr}=\left(\mathrm{11},\mathrm{13},\mathrm{17},\mathrm{19},\mathrm{23},\mathrm{31}\right)\Rightarrow\mathrm{6}\:{pieces} \\ $$$${Q}={P}\:{or}\:{Pr}\Rightarrow\mathrm{13}+\mathrm{6}=\mathrm{19}\:{pieces} \\ $$$${R}={Pr}\Rightarrow\mathrm{6}\:{pieces} \\ $$$$\left({a}\right)\:\frac{\mathrm{6}}{\mathrm{36}}=\mathrm{16}.\mathrm{6\%} \\ $$$$\left({b}\right)\:\frac{\mathrm{13}}{\mathrm{36}}=\mathrm{36}.\mathrm{1\%} \\ $$
Commented by tawa last updated on 29/Mar/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
