Question Number 77183 by jagoll last updated on 04/Jan/20

$$\mathrm{what}\:\mathrm{is}\:\mathrm{x}\: \\ $$$$\mathrm{satisfy}\:\mathrm{inequality}\: \\ $$$$\mathrm{3}^{\mathrm{x}^{\mathrm{2}} } ×\:\mathrm{5}^{\mathrm{x}−\mathrm{1}} \:\geqslant\:\mathrm{3} \\ $$
Answered by john santu last updated on 04/Jan/20
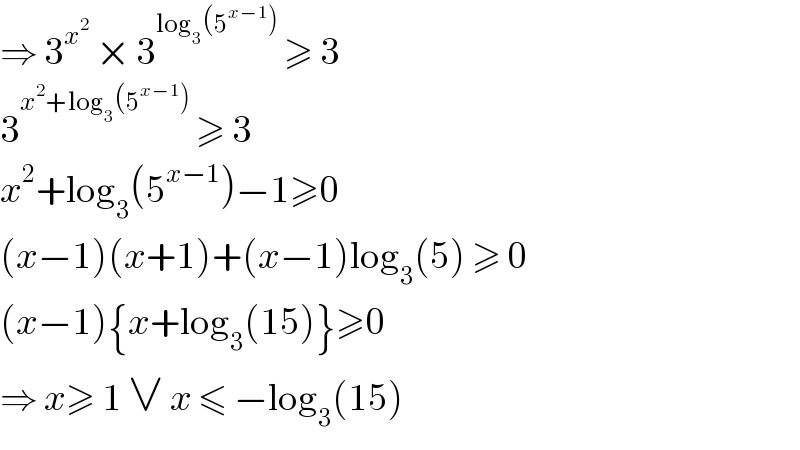
$$\Rightarrow\:\mathrm{3}^{{x}^{\mathrm{2}} } \:×\:\mathrm{3}^{\mathrm{log}_{\mathrm{3}} \left(\mathrm{5}^{{x}−\mathrm{1}} \right)} \:\geqslant\:\mathrm{3} \\ $$$$\mathrm{3}^{{x}^{\mathrm{2}} +\mathrm{log}_{\mathrm{3}} \left(\mathrm{5}^{{x}−\mathrm{1}} \right)} \:\geqslant\:\mathrm{3} \\ $$$${x}^{\mathrm{2}} +\mathrm{log}_{\mathrm{3}} \left(\mathrm{5}^{{x}−\mathrm{1}} \right)−\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)+\left({x}−\mathrm{1}\right)\mathrm{log}_{\mathrm{3}} \left(\mathrm{5}\right)\:\geqslant\:\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left\{{x}+\mathrm{log}_{\mathrm{3}} \left(\mathrm{15}\right)\right\}\geqslant\mathrm{0} \\ $$$$\Rightarrow\:{x}\geqslant\:\mathrm{1}\:\vee\:{x}\:\leqslant\:−\mathrm{log}_{\mathrm{3}} \left(\mathrm{15}\right) \\ $$
Commented by jagoll last updated on 04/Jan/20

$$\mathrm{thanks}\:\mathrm{sir} \\ $$
