Question Number 142745 by iloveisrael last updated on 05/Jun/21

Commented by MJS_new last updated on 05/Jun/21
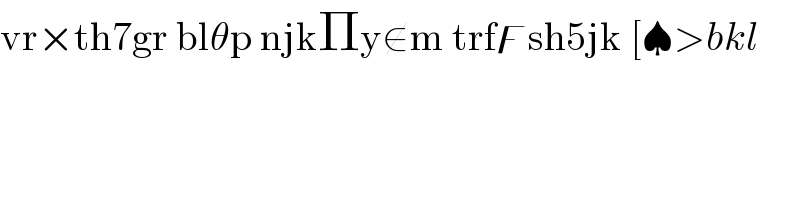
$$\mathrm{vr}×\mathrm{th7gr}\:\mathrm{bl}\theta\mathrm{p}\:\mathrm{njk}\Pi\mathrm{y}\notin\mathrm{m}\:\mathrm{trf}\digamma\mathrm{sh5jk}\:\left[\spadesuit>{bkl}\right. \\ $$
Commented by iloveisrael last updated on 05/Jun/21
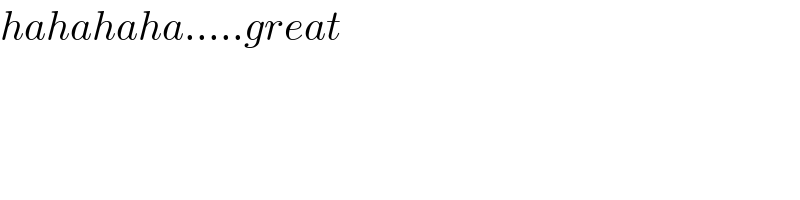
$${hahahaha}…..{great} \\ $$
Commented by iloveisrael last updated on 05/Jun/21

$$ \\ $$maybe in this forum there are members who understand Japanese
Commented by mr W last updated on 05/Jun/21
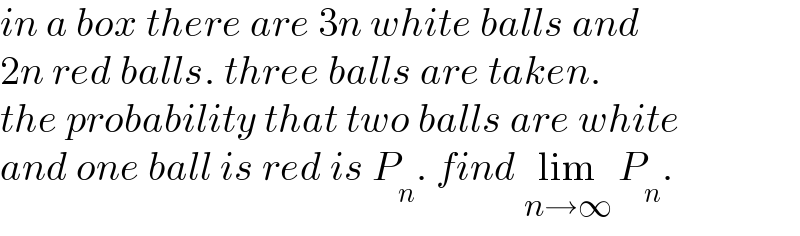
$${in}\:{a}\:{box}\:{there}\:{are}\:\mathrm{3}{n}\:{white}\:{balls}\:{and}\: \\ $$$$\mathrm{2}{n}\:{red}\:{balls}.\:{three}\:{balls}\:{are}\:{taken}. \\ $$$${the}\:{probability}\:{that}\:{two}\:{balls}\:{are}\:{white} \\ $$$${and}\:{one}\:{ball}\:{is}\:{red}\:{is}\:{P}_{{n}} .\:{find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{P}_{{n}} . \\ $$
Commented by iloveisrael last updated on 05/Jun/21
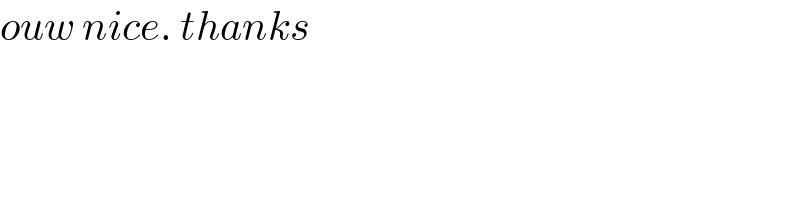
$${ouw}\:{nice}.\:{thanks} \\ $$
Commented by MJS_new last updated on 05/Jun/21
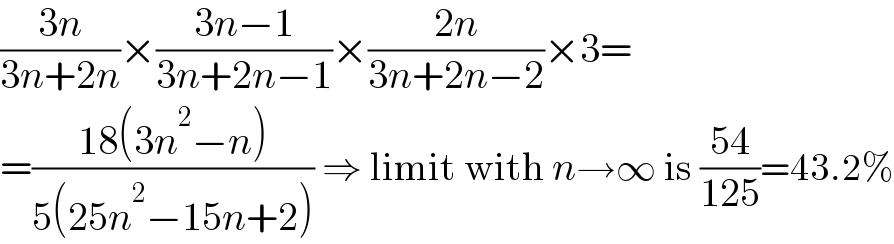
$$\frac{\mathrm{3}{n}}{\mathrm{3}{n}+\mathrm{2}{n}}×\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{3}{n}+\mathrm{2}{n}−\mathrm{1}}×\frac{\mathrm{2}{n}}{\mathrm{3}{n}+\mathrm{2}{n}−\mathrm{2}}×\mathrm{3}= \\ $$$$=\frac{\mathrm{18}\left(\mathrm{3}{n}^{\mathrm{2}} −{n}\right)}{\mathrm{5}\left(\mathrm{25}{n}^{\mathrm{2}} −\mathrm{15}{n}+\mathrm{2}\right)}\:\Rightarrow\:\mathrm{limit}\:\mathrm{with}\:{n}\rightarrow\infty\:\mathrm{is}\:\frac{\mathrm{54}}{\mathrm{125}}=\mathrm{43}.\mathrm{2\%} \\ $$
Commented by EDWIN88 last updated on 05/Jun/21

$$\mathrm{white}\:\mathrm{balls}\:=\:\mathrm{3n} \\ $$$$\mathrm{red}\:\mathrm{balls}\:=\:\mathrm{2n} \\ $$$$\mathrm{P}_{\mathrm{n}} =\:\frac{\mathrm{C}_{\mathrm{2}} ^{\:\mathrm{3n}} \:.\:\mathrm{C}_{\mathrm{1}} ^{\:\mathrm{2n}} }{\mathrm{C}_{\mathrm{3}} ^{\:\mathrm{5n}} }\:=\:\frac{\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\cancel{\mathrm{2}.\mathrm{1}}}\:.\:\frac{\cancel{\mathrm{2}n}}{\mathrm{1}}}{\frac{\mathrm{5n}\left(\mathrm{5n}−\mathrm{1}\right)\left(\mathrm{5n}−\mathrm{2}\right)}{\mathrm{3}.\mathrm{2}.\mathrm{1}}} \\ $$$$\:=\:\frac{\mathrm{18n}^{\mathrm{2}} \left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{5n}\left(\mathrm{5n}−\mathrm{1}\right)\left(\mathrm{5n}−\mathrm{2}\right)} \\ $$$$\underset{\mathrm{n}\rightarrow\:\infty} {\mathrm{lim}P}_{\mathrm{n}} =\:\underset{\mathrm{n}\rightarrow\:\infty} {\mathrm{lim}}\:\frac{\mathrm{54n}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3n}}\right)}{\mathrm{125n}^{\mathrm{3}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5n}}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{5n}}\right)} \\ $$$$\underset{\mathrm{n}\rightarrow\:\infty} {\mathrm{lim}}\:\frac{\mathrm{54}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3n}}\right)}{\mathrm{125}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5n}}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{5n}}\right)}\:=\:\frac{\mathrm{54}}{\mathrm{125}}\:\Box \\ $$
