Question Number 11770 by Nayon last updated on 31/Mar/17
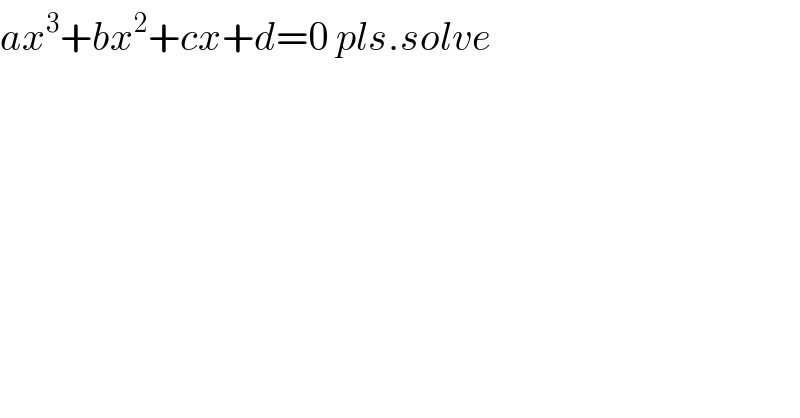
$${ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0}\:{pls}.{solve} \\ $$
Answered by Joel576 last updated on 31/Mar/17

$${f}\left({x}\right)\:=\:{x}^{\mathrm{3}} \:+\:\frac{{b}}{{a}}{x}^{\mathrm{2}} \:+\:\frac{{c}}{{a}}{x}\:+\:\frac{{d}}{{a}}\:=\:\mathrm{0}\:\:\:…\:\left({i}\right) \\ $$$$\mathrm{Let}\:{p},\:{q},\:{r}\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{from}\:{f}\left({x}\right) \\ $$$$\mathrm{We}\:\mathrm{get}: \\ $$$${f}\left({x}\right)\:=\:\left({x}\:−\:{p}\right)\left({x}\:−\:{q}\right)\left({x}\:−\:{r}\right)\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\left({x}^{\mathrm{2}} \:−\:{qx}\:−\:{px}\:+\:{pq}\right)\left({x}\:−\:{r}\right)\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{x}^{\mathrm{3}} \:−\:{rx}^{\mathrm{2}} \:−\:{qx}^{\mathrm{2}} \:+\:{qrx}\:−\:{px}^{\mathrm{2}} \:+\:{rpx}\:+\:{pqx}\:−\:{pqr} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{x}^{\mathrm{3}} \:−\:\left({p}\:+\:{q}\:+\:{r}\right){x}^{\mathrm{2}} \:+\:\left({pq}\:+\:{qr}\:+\:{rp}\right){x}\:−\:{pqr}\:=\:\mathrm{0}\:\:\:…\:\left({ii}\right) \\ $$$$\mathrm{From}\:\left({i}\right)\:\mathrm{and}\:\left({ii}\right)\:\mathrm{we}\:\mathrm{can}\:\mathrm{conclude}: \\ $$$${p}\:+\:{q}\:+\:{r}\:=\:−\frac{{b}}{{a}} \\ $$$${pq}\:+\:{qr}\:+\:{rp}\:=\:\frac{{c}}{{a}} \\ $$$${pqr}\:=\:−\frac{{d}}{{a}} \\ $$
Commented by Nayon last updated on 31/Mar/17
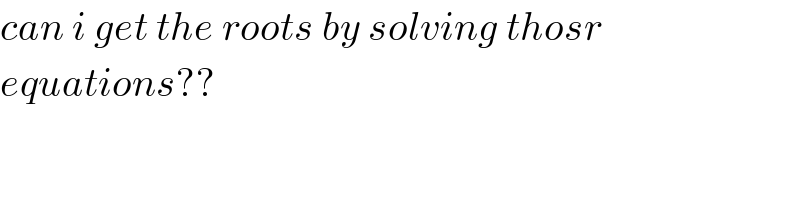
$${can}\:{i}\:{get}\:{the}\:{roots}\:{by}\:{solving}\:{thosr} \\ $$$${equations}?? \\ $$
Commented by Joel576 last updated on 31/Mar/17

Commented by Nayon last updated on 31/Mar/17
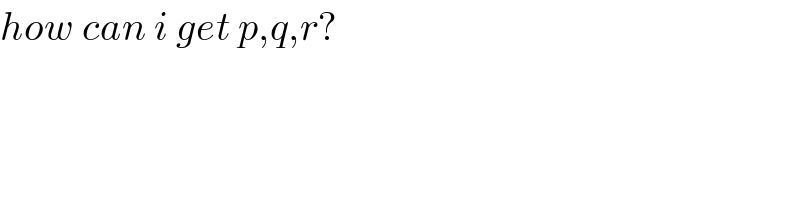
$${how}\:{can}\:{i}\:{get}\:{p},{q},{r}? \\ $$$$ \\ $$
Commented by mrW1 last updated on 31/Mar/17

$${To}\:{solve}\:{the}\:{equation}\:{system}\:{for}\:{p}, \\ $$$${q},\:{r}\:{you}\:{also}\:{need}\:{to}\:{solve}\:{an}\:{other}\:{cubic} \\ $$$${equation},\:{so}\:{you}\:{reach}\:{nothing}\:{in} \\ $$$${this}\:{way}.\: \\ $$$$ \\ $$$${To}\:{be}\:{honest},\:{we}\:{don}'{t}\:{need} \\ $$$${to}\:{reinvent}\:{the}\:{wheel}\:{again}.\:{The}\: \\ $$$${general}\:{way}\:{to}\:{solve}\:{a}\:{cubic}\:{equation}\:{of} \\ $$$${the}\:{form}\:{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}=\mathrm{0}\:{is}\:{known} \\ $$$${since}\:{hundreds}\:{of}\:{years}.\:{People}\:{have} \\ $$$${created}\:{general}\:{formulas}\:{like}\:{those}\:{above} \\ $$$${which}\:{we}\:{can}\:{use}\:{directly}.\:{The}\:{way} \\ $$$${of}\:{solution}\:{is}\:{too}\:{long}\:{to}\:{be}\:{given}\:{here}. \\ $$$${In}\:{Google}\:{you}\:{can}\:{find}\:{a}\:{lot}\:{of}\:{stuff} \\ $$$${about}\:{it}.\:{So}\:{far}\:{as}\:{I}\:{know},\:{the}\:{basic} \\ $$$${idea}\:{is}\:{to}\:{do}\:{some}\:{substitutions}\:{to}\:{put} \\ $$$${the}\:{equation}\:{into}\:{a}\:{new}\:{form}\:{whose} \\ $$$${solution}\:{is}\:{known}. \\ $$$${I}\:{can}\:{give}\:{you}\:{an}\:{interesting}\:{link} \\ $$$${which}\:{contains}\:{a}\:{detailed}\:{description}. \\ $$
Commented by mrW1 last updated on 31/Mar/17

