Question Number 77323 by Boyka last updated on 05/Jan/20

Commented by Tony Lin last updated on 05/Jan/20
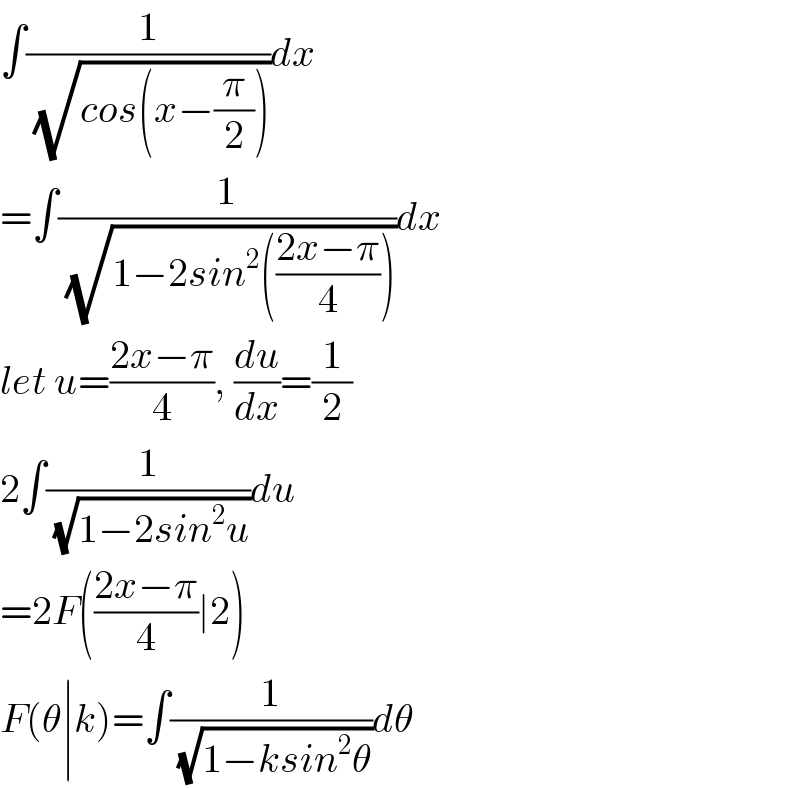
$$\int\frac{\mathrm{1}}{\:\sqrt{{cos}\left({x}−\frac{\pi}{\mathrm{2}}\right)}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\mathrm{2}{x}−\pi}{\mathrm{4}}\right)}}{dx} \\ $$$${let}\:{u}=\frac{\mathrm{2}{x}−\pi}{\mathrm{4}},\:\frac{{du}}{{dx}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {u}}}{du} \\ $$$$=\mathrm{2}{F}\left(\frac{\mathrm{2}{x}−\pi}{\mathrm{4}}\mid\mathrm{2}\right) \\ $$$${F}\left(\theta\mid{k}\right)=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{ksin}^{\mathrm{2}} \theta}}{d}\theta \\ $$
Commented by MJS last updated on 05/Jan/20

$$\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{an}\:\mathrm{incomplete}\:\mathrm{elliptic}\:\mathrm{integral} \\ $$$$\mathrm{of}\:\mathrm{first}\:\mathrm{order} \\ $$$$\int\frac{{dx}}{\:\sqrt{\mathrm{sin}\:{x}}}=\mathrm{2F}\:\left(\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\mid\mathrm{2}\right) \\ $$$$\mathrm{look}\:\mathrm{it}\:\mathrm{up}\:\mathrm{on}\:\mathrm{the}\:\mathrm{web} \\ $$
