Question Number 77346 by BK last updated on 05/Jan/20
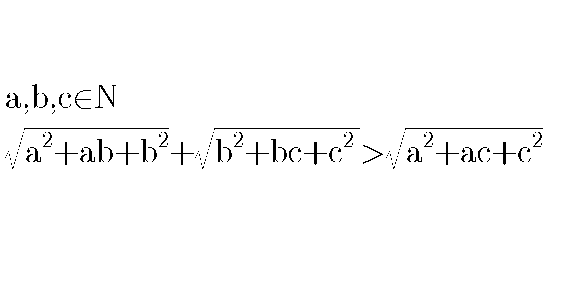
Commented by BK last updated on 05/Jan/20

$$\mathrm{prove}\:\mathrm{that} \\ $$
Commented by mind is power last updated on 05/Jan/20
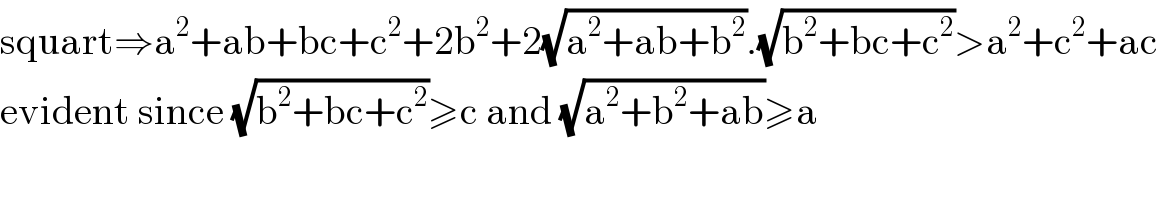
$$\mathrm{squart}\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{bc}+\mathrm{c}^{\mathrm{2}} +\mathrm{2b}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{ab}+\mathrm{b}^{\mathrm{2}} }.\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{bc}+\mathrm{c}^{\mathrm{2}} }>\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{ac} \\ $$$$\mathrm{evident}\:\mathrm{since}\:\sqrt{\mathrm{b}^{\mathrm{2}} +\mathrm{bc}+\mathrm{c}^{\mathrm{2}} }\geqslant\mathrm{c}\:\mathrm{and}\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{ab}}\geqslant\mathrm{a} \\ $$
Commented by BK last updated on 05/Jan/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
