Question Number 11823 by Joel576 last updated on 01/Apr/17
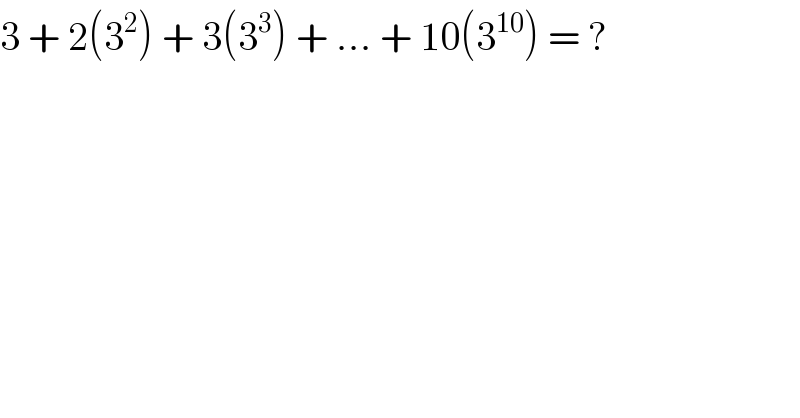
$$\mathrm{3}\:+\:\mathrm{2}\left(\mathrm{3}^{\mathrm{2}} \right)\:+\:\mathrm{3}\left(\mathrm{3}^{\mathrm{3}} \right)\:+\:…\:+\:\mathrm{10}\left(\mathrm{3}^{\mathrm{10}} \right)\:=\:? \\ $$
Answered by ajfour last updated on 02/Apr/17
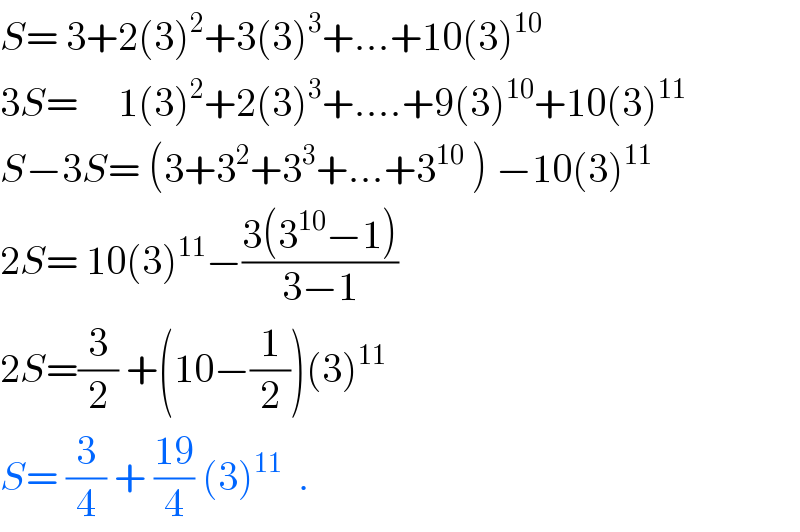
$${S}=\:\mathrm{3}+\mathrm{2}\left(\mathrm{3}\right)^{\mathrm{2}} +\mathrm{3}\left(\mathrm{3}\right)^{\mathrm{3}} +…+\mathrm{10}\left(\mathrm{3}\right)^{\mathrm{10}} \\ $$$$\mathrm{3}{S}=\:\:\:\:\:\mathrm{1}\left(\mathrm{3}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}\right)^{\mathrm{3}} +….+\mathrm{9}\left(\mathrm{3}\right)^{\mathrm{10}} +\mathrm{10}\left(\mathrm{3}\right)^{\mathrm{11}} \\ $$$${S}−\mathrm{3}{S}=\:\left(\mathrm{3}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +…+\mathrm{3}^{\mathrm{10}} \:\right)\:−\mathrm{10}\left(\mathrm{3}\right)^{\mathrm{11}} \\ $$$$\mathrm{2}{S}=\:\mathrm{10}\left(\mathrm{3}\right)^{\mathrm{11}} −\frac{\mathrm{3}\left(\mathrm{3}^{\mathrm{10}} −\mathrm{1}\right)}{\mathrm{3}−\mathrm{1}} \\ $$$$\mathrm{2}{S}=\frac{\mathrm{3}}{\mathrm{2}}\:+\left(\mathrm{10}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left(\mathrm{3}\right)^{\mathrm{11}} \\ $$$${S}=\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{19}}{\mathrm{4}}\:\left(\mathrm{3}\right)^{\mathrm{11}} \:\:. \\ $$
Commented by Joel576 last updated on 02/Apr/17
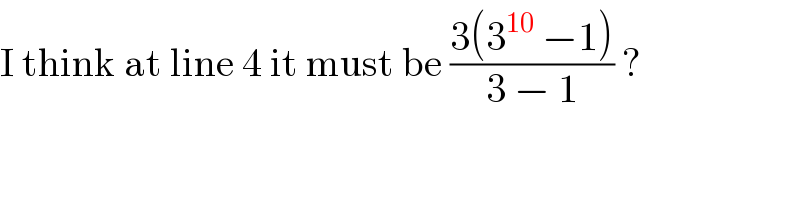
$$\mathrm{I}\:\mathrm{think}\:\mathrm{at}\:\mathrm{line}\:\mathrm{4}\:\mathrm{it}\:\mathrm{must}\:\mathrm{be}\:\frac{\mathrm{3}\left(\mathrm{3}^{\mathrm{10}} \:−\mathrm{1}\right)}{\mathrm{3}\:−\:\mathrm{1}}\:? \\ $$
Commented by ajfour last updated on 02/Apr/17
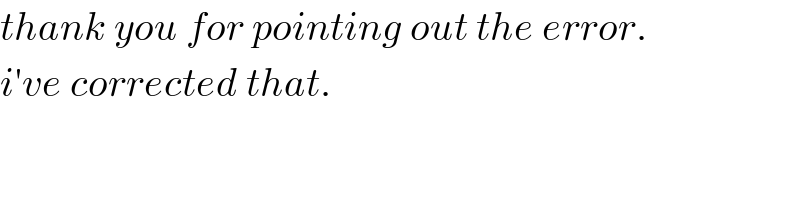
$${thank}\:{you}\:{for}\:{pointing}\:{out}\:{the}\:{error}. \\ $$$${i}'{ve}\:{corrected}\:{that}.\: \\ $$
Commented by Joel576 last updated on 02/Apr/17

$${you}'{re}\:{welcome} \\ $$
