Menu Close

Q-141663-by-ajfour-sir-reposted-x-2-x-12-x-15-k-x-16-k-gt-0-Find-x-in-terms-of-k-

Tinku Tara 0 Comments
Pin




Question Number 142939 by Rasheed.Sindhi last updated on 07/Jun/21
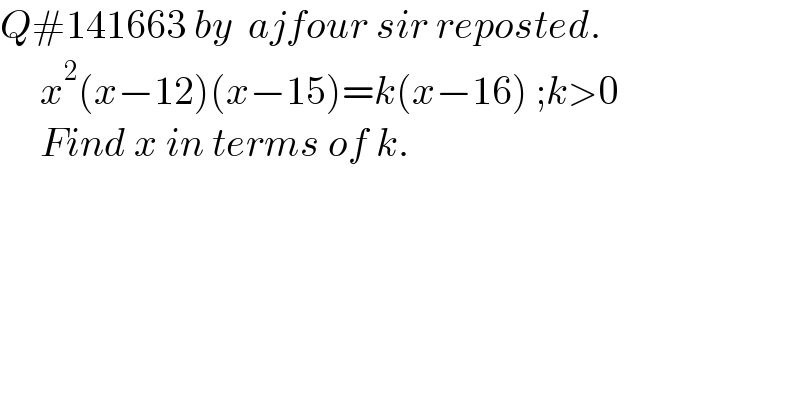
Q#141663 by ajfour sir reposted. x^2 (x−12)(x−15)=k(x−16) ;k>0 Find x in terms of k.
$${Q}#\mathrm{141663}\:{by}\:\:{ajfour}\:{sir}\:{reposted}. \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)={k}\left({x}−\mathrm{16}\right)\:;{k}>\mathrm{0} \\ $$$$\:\:\:\:\:{Find}\:{x}\:{in}\:{terms}\:{of}\:{k}. \\ $$
Answered by Rasheed.Sindhi last updated on 07/Jun/21
{x^2 (x−12)(x−15)}/(x−16)=k Quotient is k with no remainder. Let p(x)=x^2 (x^2 −27x+180) =x^4 −27x^3 +180x^2 +0x+0 By synthetic division: determinant (((16)),1,(−27),(180),0,0),(,,( 16),(−176),(64),(1024)),(,1,(−11),( 4),(64),(1024))) p(x)=Q(x)D(x)+R x^2 (x−12)(x−15)= (x^3 −11x^2 +4x+64)(x−16)+1024 Neither the quotient is constant nor the remainder is zero ∀ x So this proves that the equation has no solution.
$$\left\{{x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)\right\}/\left({x}−\mathrm{16}\right)={k} \\ $$$${Quotient}\:{is}\:{k}\:{with}\:{no}\:{remainder}. \\ $$$${Let}\:{p}\left({x}\right)={x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{27}{x}+\mathrm{180}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{4}} −\mathrm{27}{x}^{\mathrm{3}} +\mathrm{180}{x}^{\mathrm{2}} +\mathrm{0}{x}+\mathrm{0} \\ $$$${By}\:{synthetic}\:{division}: \\ $$$$\begin{array}{|c|c|c|}{\left.\mathrm{16}\right)}&\hline{\mathrm{1}}&\hline{−\mathrm{27}}&\hline{\mathrm{180}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}\\{}&\hline{}&\hline{\:\:\:\:\mathrm{16}}&\hline{−\mathrm{176}}&\hline{\mathrm{64}}&\hline{\mathrm{1024}}\\{}&\hline{\mathrm{1}}&\hline{−\mathrm{11}}&\hline{\:\:\:\:\:\mathrm{4}}&\hline{\mathrm{64}}&\hline{\mathrm{1024}}\\\hline\end{array} \\ $$$${p}\left({x}\right)={Q}\left({x}\right){D}\left({x}\right)+{R} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)= \\ $$$$\:\left({x}^{\mathrm{3}} −\mathrm{11}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{64}\right)\left({x}−\mathrm{16}\right)+\mathrm{1024} \\ $$$${Neither}\:{the}\:{quotient}\:{is}\:{constant} \\ $$$${nor}\:{the}\:{remainder}\:{is}\:{zero}\:\forall\:{x} \\ $$$${So}\:{this}\:{proves}\:{that}\:{the}\:{equation} \\ $$$${has}\:{no}\:{solution}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by mr W last updated on 07/Jun/21
i think it′s wrong somewhere sir. y=x^2 (x−12)(x−15) is a curve passing through (0,0),(12,0) and (15,0) y=k(x−16) is a line passing through (16,0) with inclination k. from (16,0) we can draw two tangent lines to the curve, say these tangent lines have inclination k_1 and k_2 . we know for k≤k_1 or k≥k_2 , the line y=k(x−16) intersects the curve at least at one point and at most at four points. that means for k≤k_1 or k≥k_2 , the equation x^2 (x−12)(x−15)=k(x−16) has at least one solution and at most four solutions.
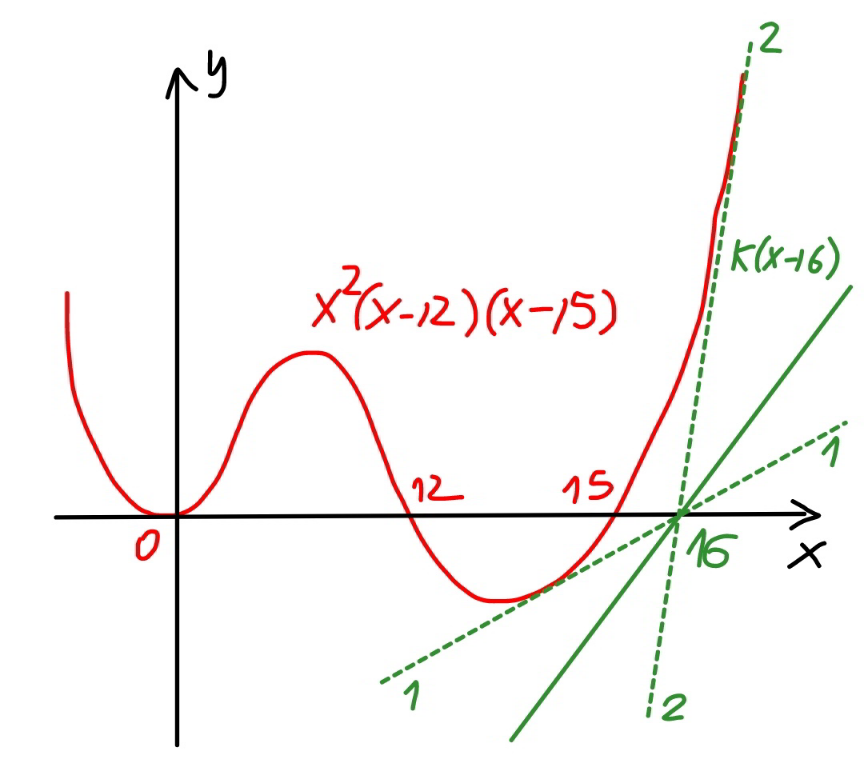
$${i}\:{think}\:{it}'{s}\:{wrong}\:{somewhere}\:{sir}. \\ $$$${y}={x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)\:{is}\:{a}\:{curve}\:{passing} \\ $$$${through}\:\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{12},\mathrm{0}\right)\:{and}\:\left(\mathrm{15},\mathrm{0}\right) \\ $$$${y}={k}\left({x}−\mathrm{16}\right)\:{is}\:{a}\:{line}\:{passing}\:{through} \\ $$$$\left(\mathrm{16},\mathrm{0}\right)\:{with}\:{inclination}\:{k}. \\ $$$${from}\:\left(\mathrm{16},\mathrm{0}\right)\:{we}\:{can}\:{draw}\:{two}\:{tangent} \\ $$$${lines}\:{to}\:{the}\:{curve},\:{say}\:{these}\:{tangent} \\ $$$${lines}\:{have}\:{inclination}\:{k}_{\mathrm{1}} \:{and}\:{k}_{\mathrm{2}} . \\ $$$${we}\:{know}\:{for}\:{k}\leqslant{k}_{\mathrm{1}} \:{or}\:{k}\geqslant{k}_{\mathrm{2}} ,\:{the}\:{line} \\ $$$${y}={k}\left({x}−\mathrm{16}\right)\:{intersects}\:{the}\:{curve}\:{at} \\ $$$${least}\:{at}\:{one}\:{point}\:{and}\:{at}\:{most}\:{at} \\ $$$${four}\:{points}.\:{that}\:{means}\:{for} \\ $$$${k}\leqslant{k}_{\mathrm{1}} \:{or}\:{k}\geqslant{k}_{\mathrm{2}} ,\:{the}\:{equation} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)={k}\left({x}−\mathrm{16}\right)\:{has} \\ $$$${at}\:{least}\:{one}\:{solution}\:{and}\:{at}\:{most} \\ $$$${four}\:{solutions}. \\ $$
Commented by mr W last updated on 07/Jun/21
Commented by Rasheed.Sindhi last updated on 08/Jun/21
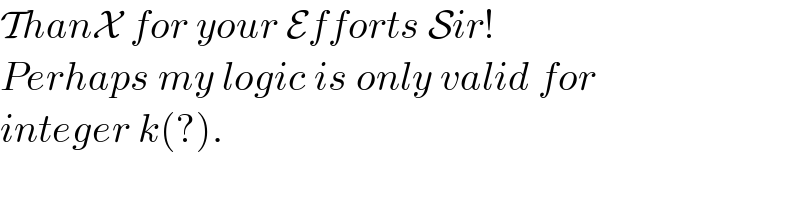
ThanX for your Efforts Sir! Perhaps my logic is only valid for integer k(?).
$$\mathcal{T}{han}\mathcal{X}\:{for}\:{your}\:\mathcal{E}{fforts}\:\mathcal{S}{ir}! \\ $$$${Perhaps}\:{my}\:{logic}\:{is}\:{only}\:{valid}\:{for} \\ $$$${integer}\:{k}\left(?\right). \\ $$
Commented by mr W last updated on 08/Jun/21
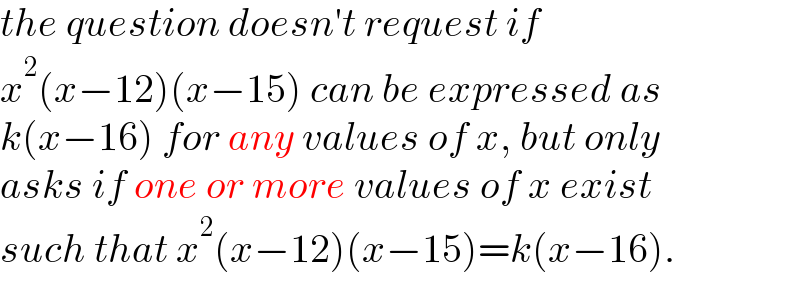
the question doesn′t request if x^2 (x−12)(x−15) can be expressed as k(x−16) for any values of x, but only asks if one or more values of x exist such that x^2 (x−12)(x−15)=k(x−16).
$${the}\:{question}\:{doesn}'{t}\:{request}\:{if} \\ $$$${x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)\:{can}\:{be}\:{expressed}\:{as} \\ $$$${k}\left({x}−\mathrm{16}\right)\:{for}\:{any}\:{values}\:{of}\:{x},\:{but}\:{only} \\ $$$${asks}\:{if}\:{one}\:{or}\:{more}\:{values}\:{of}\:{x}\:{exist} \\ $$$${such}\:{that}\:{x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)={k}\left({x}−\mathrm{16}\right). \\ $$
Commented by Rasheed.Sindhi last updated on 08/Jun/21
OK Sir, ThanX again.
$$\mathcal{OK}\:\mathcal{S}{ir},\:\mathcal{T}{han}\mathcal{X}\:{again}. \\ $$
Answered by Rasheed.Sindhi last updated on 07/Jun/21
x^2 (x−12)(x−15)=k(x−16) ;k>0 This means : When x^2 (x−12)(x−15) is divided by x−16, The quotient is k(>0) and the remainder is 0 But we can verify that the remainder R is: R=(16)^2 (16−12)(16−15) =256.4.1=1024≠0 So for any value of x the remainder can′t be zero. This proves that the above equation can′t be solved (even in terms of k>0.)
$$\:\:\:\:\:{x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)={k}\left({x}−\mathrm{16}\right)\:;{k}>\mathrm{0} \\ $$$${This}\:{means}\:: \\ $$$$\:\:\:{When}\:{x}^{\mathrm{2}} \left({x}−\mathrm{12}\right)\left({x}−\mathrm{15}\right)\:{is}\:{divided} \\ $$$${by}\:{x}−\mathrm{16},\:{The}\:{quotient}\:{is}\:{k}\left(>\mathrm{0}\right)\:{and} \\ $$$${the}\:{remainder}\:{is}\:\mathrm{0} \\ $$$${But}\:{we}\:{can}\:{verify}\:{that}\:{the}\:{remainder} \\ $$$${R}\:{is}: \\ $$$$\:\:\:\:\:\:\:{R}=\left(\mathrm{16}\right)^{\mathrm{2}} \left(\mathrm{16}−\mathrm{12}\right)\left(\mathrm{16}−\mathrm{15}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{256}.\mathrm{4}.\mathrm{1}=\mathrm{1024}\neq\mathrm{0} \\ $$$${So}\:{for}\:{any}\:{value}\:{of}\:{x}\:{the}\:{remainder} \\ $$$$\boldsymbol{{can}}'\boldsymbol{{t}}\:\boldsymbol{{be}}\:\boldsymbol{{zero}}. \\ $$$${This}\:{proves}\:{that}\:{the}\:{above}\:{equation} \\ $$$${can}'{t}\:{be}\:{solved}\:\left({even}\:{in}\:{terms}\:{of}\:{k}>\mathrm{0}.\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *