Question-77565

Question Number 77565 by TawaTawa last updated on 07/Jan/20

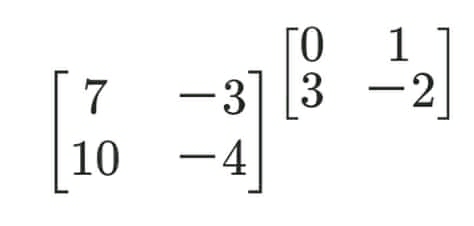
Commented by MJS last updated on 07/Jan/20

I don′t think that A^B for matrices A, B is defined. I only know A^n with n∈N; A^(−n) is only possible if the inverse matrix A^(−1) exists and is then defined as (A^(−1) )^n . A^(p/q) is only possible if A can be diagonalized and the elements of the diagonal all are ≥0. we find the diagonal matrix if a matrix T exists with A=T×D×T^(−1) in this case A^n =T×D^n ×T^(−1) and in some cases A^(p/q) =T×D^(p/q) ×T^(−1)

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{that}\:{A}^{{B}} \:\mathrm{for}\:\mathrm{matrices}\:{A},\:{B}\:\mathrm{is} \\ $$$$\mathrm{defined}.\:\mathrm{I}\:\mathrm{only}\:\mathrm{know}\:{A}^{{n}} \:\mathrm{with}\:{n}\in\mathbb{N};\:{A}^{−{n}} \:\mathrm{is} \\ $$$$\mathrm{only}\:\mathrm{possible}\:\mathrm{if}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{matrix}\:{A}^{−\mathrm{1}} \:\mathrm{exists} \\ $$$$\mathrm{and}\:\mathrm{is}\:\mathrm{then}\:\mathrm{defined}\:\mathrm{as}\:\left({A}^{−\mathrm{1}} \right)^{{n}} .\:{A}^{\frac{{p}}{{q}}} \:\mathrm{is}\:\mathrm{only} \\ $$$$\mathrm{possible}\:\mathrm{if}\:{A}\:\mathrm{can}\:\mathrm{be}\:\mathrm{diagonalized}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{elements}\:\mathrm{of}\:\mathrm{the}\:\mathrm{diagonal}\:\mathrm{all}\:\mathrm{are}\:\geqslant\mathrm{0}.\:\mathrm{we}\:\mathrm{find} \\ $$$$\mathrm{the}\:\mathrm{diagonal}\:\mathrm{matrix}\:\mathrm{if}\:\mathrm{a}\:\mathrm{matrix}\:{T}\:\mathrm{exists}\:\mathrm{with} \\ $$$${A}={T}×{D}×{T}^{−\mathrm{1}} \:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{A}^{{n}} ={T}×{D}^{{n}} ×{T}^{−\mathrm{1}} \\ $$$$\mathrm{and}\:\mathrm{in}\:\mathrm{some}\:\mathrm{cases}\:{A}^{\frac{{p}}{{q}}} ={T}×{D}^{\frac{{p}}{{q}}} ×{T}^{−\mathrm{1}} \\ $$

Commented by TawaTawa last updated on 07/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\:\mathrm{appreciate} \\ $$

Commented by TawaTawa last updated on 08/Jan/20

$$\mathrm{Sir}\:\mathrm{what}\:\mathrm{if}\:\mathrm{the}\:\mathrm{power}\:\mathrm{is}\:\mathrm{a}\:\mathrm{determinant}. \\ $$

Commented by TawaTawa last updated on 08/Jan/20

[((7 − 3)),((10 −4)) ]^ determinant (((0 1)),((3 −2)))

$$\:\:\begin{bmatrix}{\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\mathrm{3}}\\{\mathrm{10}\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}}\end{bmatrix}^{\begin{vmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:−\mathrm{2}}\end{vmatrix}} \\ $$

Commented by MJS last updated on 08/Jan/20

det determinant ((0,1),(3,(−2)))=−3 [(7,(−3)),((10),(−4)) ]^(−1) = [((−2),(3/2)),((−5),(7/2)) ] [((−2),(3/2)),((−5),(7/2)) ]^3 = [((−17/4),(21/8)),((−35/4),(43/8)) ]

$$\mathrm{det}\begin{vmatrix}{\mathrm{0}}&{\mathrm{1}}\\{\mathrm{3}}&{−\mathrm{2}}\end{vmatrix}=−\mathrm{3} \\ $$$$\begin{bmatrix}{\mathrm{7}}&{−\mathrm{3}}\\{\mathrm{10}}&{−\mathrm{4}}\end{bmatrix}^{−\mathrm{1}} =\begin{bmatrix}{−\mathrm{2}}&{\mathrm{3}/\mathrm{2}}\\{−\mathrm{5}}&{\mathrm{7}/\mathrm{2}}\end{bmatrix} \\ $$$$\begin{bmatrix}{−\mathrm{2}}&{\mathrm{3}/\mathrm{2}}\\{−\mathrm{5}}&{\mathrm{7}/\mathrm{2}}\end{bmatrix}^{\mathrm{3}} =\begin{bmatrix}{−\mathrm{17}/\mathrm{4}}&{\mathrm{21}/\mathrm{8}}\\{−\mathrm{35}/\mathrm{4}}&{\mathrm{43}/\mathrm{8}}\end{bmatrix} \\ $$

Commented by TawaTawa last updated on 08/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply