Question Number 143114 by bounhome last updated on 10/Jun/21
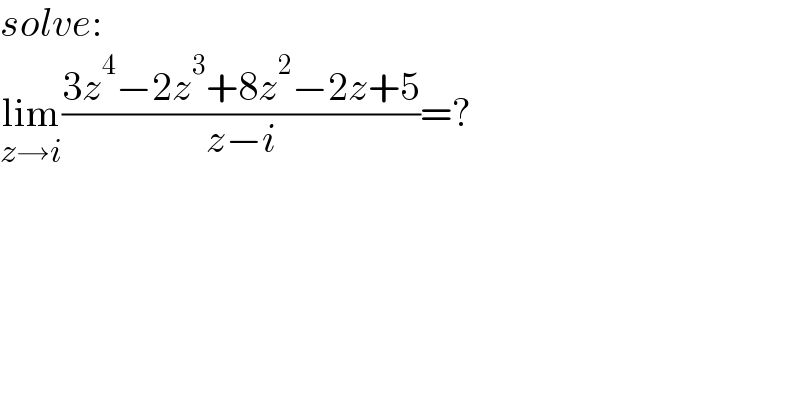
$${solve}: \\ $$$$\underset{{z}\rightarrow{i}} {\mathrm{lim}}\frac{\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}}{{z}−{i}}=? \\ $$
Answered by liberty last updated on 10/Jun/21
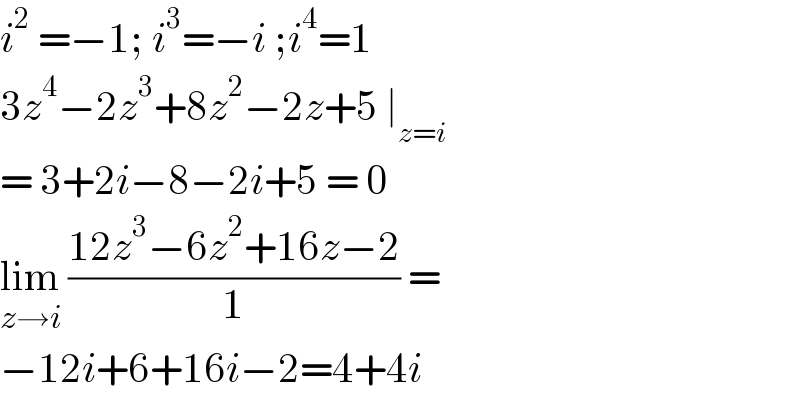
$${i}^{\mathrm{2}} \:=−\mathrm{1};\:{i}^{\mathrm{3}} =−{i}\:;{i}^{\mathrm{4}} =\mathrm{1} \\ $$$$\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}\:\mid_{{z}={i}} \\ $$$$=\:\mathrm{3}+\mathrm{2}{i}−\mathrm{8}−\mathrm{2}{i}+\mathrm{5}\:=\:\mathrm{0} \\ $$$$\underset{{z}\rightarrow{i}} {\mathrm{lim}}\:\frac{\mathrm{12}{z}^{\mathrm{3}} −\mathrm{6}{z}^{\mathrm{2}} +\mathrm{16}{z}−\mathrm{2}}{\mathrm{1}}\:= \\ $$$$−\mathrm{12}{i}+\mathrm{6}+\mathrm{16}{i}−\mathrm{2}=\mathrm{4}+\mathrm{4}{i}\: \\ $$
