Question Number 12047 by Joel576 last updated on 10/Apr/17
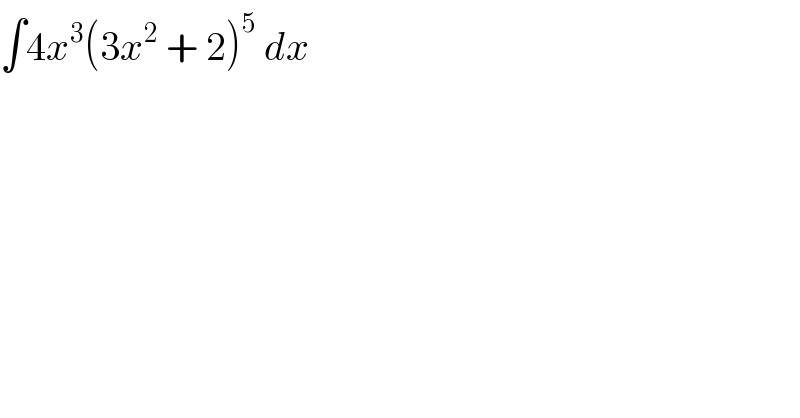
$$\int\mathrm{4}{x}^{\mathrm{3}} \left(\mathrm{3}{x}^{\mathrm{2}} \:+\:\mathrm{2}\right)^{\mathrm{5}} \:{dx} \\ $$
Commented by Joel576 last updated on 10/Apr/17

Answered by sma3l2996 last updated on 10/Apr/17
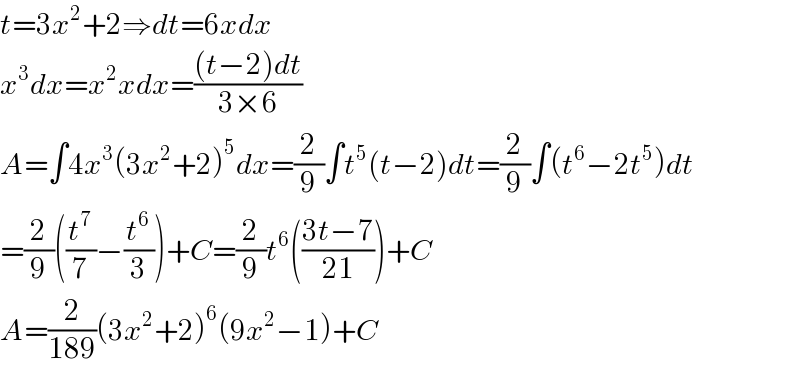
$${t}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\Rightarrow{dt}=\mathrm{6}{xdx} \\ $$$${x}^{\mathrm{3}} {dx}={x}^{\mathrm{2}} {xdx}=\frac{\left({t}−\mathrm{2}\right){dt}}{\mathrm{3}×\mathrm{6}} \\ $$$${A}=\int\mathrm{4}{x}^{\mathrm{3}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{5}} {dx}=\frac{\mathrm{2}}{\mathrm{9}}\int{t}^{\mathrm{5}} \left({t}−\mathrm{2}\right){dt}=\frac{\mathrm{2}}{\mathrm{9}}\int\left({t}^{\mathrm{6}} −\mathrm{2}{t}^{\mathrm{5}} \right){dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{9}}\left(\frac{{t}^{\mathrm{7}} }{\mathrm{7}}−\frac{{t}^{\mathrm{6}} }{\mathrm{3}}\right)+{C}=\frac{\mathrm{2}}{\mathrm{9}}{t}^{\mathrm{6}} \left(\frac{\mathrm{3}{t}−\mathrm{7}}{\mathrm{21}}\right)+{C} \\ $$$${A}=\frac{\mathrm{2}}{\mathrm{189}}\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{6}} \left(\mathrm{9}{x}^{\mathrm{2}} −\mathrm{1}\right)+{C} \\ $$
Commented by Joel576 last updated on 11/Apr/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by sma3l2996 last updated on 11/Apr/17

$${you}\:{welcome} \\ $$
