Question Number 143296 by lapache last updated on 12/Jun/21
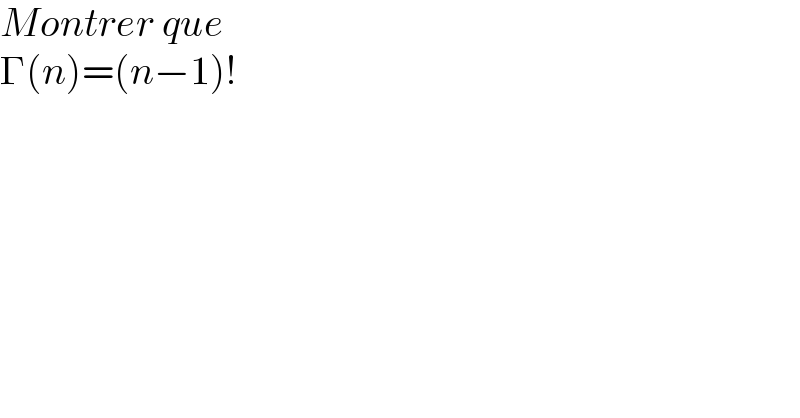
$${Montrer}\:{que} \\ $$$$\Gamma\left({n}\right)=\left({n}−\mathrm{1}\right)! \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 12/Jun/21
![By definition Γ(z) = ∫_0 ^∞ t^(z−1) e^(−t) dt If z = n∈N : Γ(n) = ∫_0 ^∞ t^(n−1) e^(−t) dt Γ(n) = ∫_0 ^∞ 1×t^(n−1) e^(−t) dt Γ(n) = [t.t^(n−1) e^(−t) ]_0 ^∞ −∫_0 ^∞ t[(n−1)t^(n−2) −t^(n−1) ]e^(−t) dt Γ(n) = −(n−1)∫_0 ^∞ t^(n−1) e^(−t) dt+∫_0 ^∞ t^n e^(−t) dt Γ(n) = −(n−1)Γ(n)+Γ(n+1) Γ(n+1) = nΓ(n) Γ(n+1) = n(n−1)Γ(n−1) ... Γ(n+1) = n!Γ(1) Γ(1) = ∫_0 ^∞ t^(1−1) e^(−t) dt = ∫_0 ^∞ e^(−t) dt Γ(1) = [−e^(−t) ]_0 ^∞ = 1 Γ(n+1) = n!Γ(1) = n!×1 = n! and of course Γ(n) = (n−1)!](https://www.tinkutara.com/question/Q143300.png)
$$\mathrm{By}\:\mathrm{definition}\:\Gamma\left({z}\right)\:=\:\int_{\mathrm{0}} ^{\infty} {t}^{{z}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\mathrm{If}\:{z}\:=\:{n}\in\mathbb{N}\:: \\ $$$$\Gamma\left({n}\right)\:=\:\int_{\mathrm{0}} ^{\infty} {t}^{{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\Gamma\left({n}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \mathrm{1}×{t}^{{n}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\Gamma\left({n}\right)\:=\:\left[{t}.{t}^{{n}−\mathrm{1}} {e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} \\ $$$$−\int_{\mathrm{0}} ^{\infty} {t}\left[\left({n}−\mathrm{1}\right){t}^{{n}−\mathrm{2}} −{t}^{{n}−\mathrm{1}} \right]{e}^{−{t}} {dt} \\ $$$$\Gamma\left({n}\right)\:=\:−\left({n}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} {t}^{{n}−\mathrm{1}} {e}^{−{t}} {dt}+\int_{\mathrm{0}} ^{\infty} {t}^{{n}} {e}^{−{t}} {dt} \\ $$$$\Gamma\left({n}\right)\:=\:−\left({n}−\mathrm{1}\right)\Gamma\left({n}\right)+\Gamma\left({n}+\mathrm{1}\right) \\ $$$$\Gamma\left({n}+\mathrm{1}\right)\:=\:{n}\Gamma\left({n}\right) \\ $$$$\Gamma\left({n}+\mathrm{1}\right)\:=\:{n}\left({n}−\mathrm{1}\right)\Gamma\left({n}−\mathrm{1}\right) \\ $$$$… \\ $$$$\Gamma\left({n}+\mathrm{1}\right)\:=\:{n}!\Gamma\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\Gamma\left(\mathrm{1}\right)\:=\:\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{1}−\mathrm{1}} {e}^{−{t}} {dt}\:=\:\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {dt} \\ $$$$\Gamma\left(\mathrm{1}\right)\:=\:\left[−{e}^{−{t}} \right]_{\mathrm{0}} ^{\infty} \:=\:\mathrm{1} \\ $$$$ \\ $$$$\Gamma\left({n}+\mathrm{1}\right)\:=\:{n}!\Gamma\left(\mathrm{1}\right)\:=\:{n}!×\mathrm{1}\:=\:{n}! \\ $$$$ \\ $$$$\mathrm{and}\:\mathrm{of}\:\mathrm{course}\:\:\Gamma\left({n}\right)\:=\:\left({n}−\mathrm{1}\right)! \\ $$
Answered by Ar Brandon last updated on 12/Jun/21
![I=Γ(n+1)=n! I=∫_0 ^∞ t^n e^(−t) dt, u(t)=t^n , v′(t)=e^(−t) =[−t^n e^(−t) +n∫t^(n−1) e^(−t) dt]_0 ^∞ =n∫_0 ^∞ t^(n−1) e^(−t) dt =n[−t^(n−1) e^(−t) +(n−1)∫t^(n−2) e^(−t) dt]_0 ^∞ =n(n−1)∫_0 ^∞ t^(n−2) e^(−t) dt =n(n−1)[−t^(n−2) e^(−t) +(n−2)∫t^(n−3) e^(−t) dt]_0 ^∞ =n(n−1)(n−2)∫_0 ^∞ t^(n−3) e^(−t) dt =n(n−1)(n−2)...3×2×∫_0 ^∞ te^(−t) dt=n!](https://www.tinkutara.com/question/Q143309.png)
$$\mathrm{I}=\Gamma\left(\mathrm{n}+\mathrm{1}\right)=\mathrm{n}! \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{n}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt},\:\mathrm{u}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{n}} ,\:\mathrm{v}'\left(\mathrm{t}\right)=\mathrm{e}^{−\mathrm{t}} \\ $$$$\:\:=\left[−\mathrm{t}^{\mathrm{n}} \mathrm{e}^{−\mathrm{t}} +\mathrm{n}\int\mathrm{t}^{\mathrm{n}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt}\right]_{\mathrm{0}} ^{\infty} =\mathrm{n}\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{n}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$\:\:=\mathrm{n}\left[−\mathrm{t}^{\mathrm{n}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} +\left(\mathrm{n}−\mathrm{1}\right)\int\mathrm{t}^{\mathrm{n}−\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt}\right]_{\mathrm{0}} ^{\infty} =\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{n}−\mathrm{2}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$\:\:=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left[−\mathrm{t}^{\mathrm{n}−\mathrm{2}} \mathrm{e}^{−\mathrm{t}} +\left(\mathrm{n}−\mathrm{2}\right)\int\mathrm{t}^{\mathrm{n}−\mathrm{3}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt}\right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{n}−\mathrm{3}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$\:\:=\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)…\mathrm{3}×\mathrm{2}×\int_{\mathrm{0}} ^{\infty} \mathrm{te}^{−\mathrm{t}} \mathrm{dt}=\mathrm{n}! \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jun/21
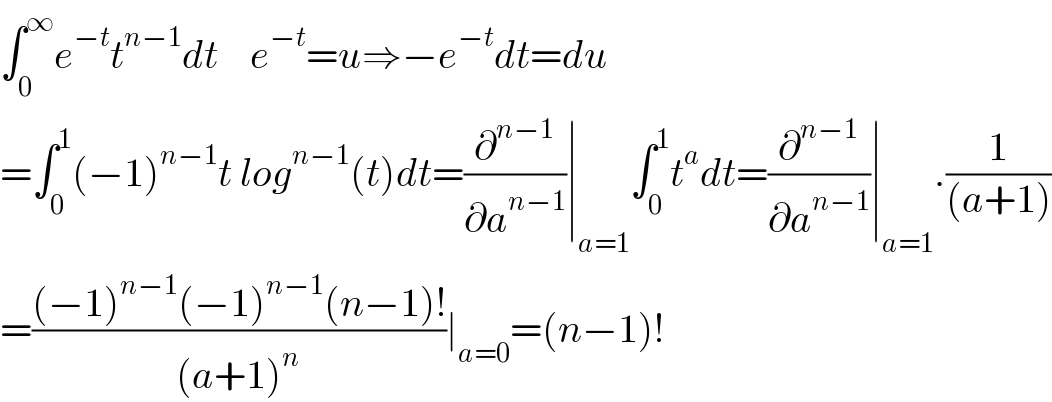
$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {t}^{{n}−\mathrm{1}} {dt}\:\:\:\:{e}^{−{t}} ={u}\Rightarrow−{e}^{−{t}} {dt}={du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}\:{log}^{{n}−\mathrm{1}} \left({t}\right){dt}=\frac{\partial^{{n}−\mathrm{1}} }{\partial{a}^{{n}−\mathrm{1}} }\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{a}} {dt}=\frac{\partial^{{n}−\mathrm{1}} }{\partial{a}^{{n}−\mathrm{1}} }\mid_{{a}=\mathrm{1}} .\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left({n}−\mathrm{1}\right)!}{\left({a}+\mathrm{1}\right)^{{n}} }\mid_{{a}=\mathrm{0}} =\left({n}−\mathrm{1}\right)! \\ $$
