Question Number 77778 by Dah Solu Tion last updated on 10/Jan/20

$$\int\frac{{cosx}}{\mathrm{2}−{cosx}}{dx} \\ $$$$ \\ $$
Commented by Tony Lin last updated on 10/Jan/20
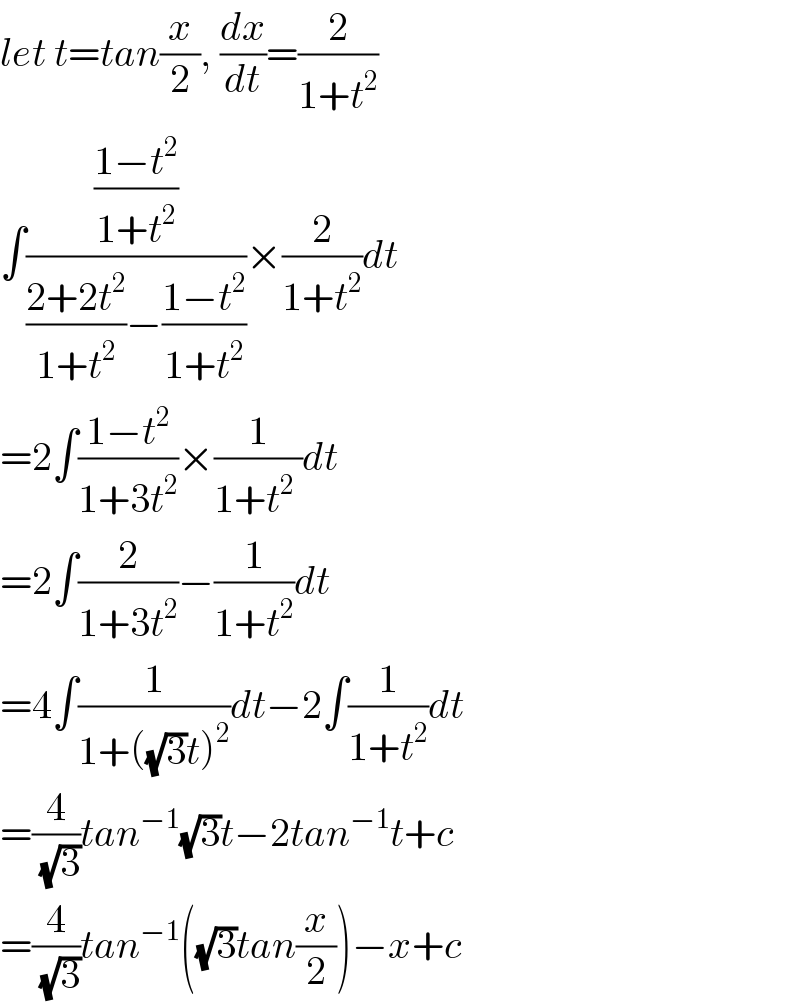
$${let}\:{t}={tan}\frac{{x}}{\mathrm{2}},\:\frac{{dx}}{{dt}}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\int\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{2}+\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} \:}{dt} \\ $$$$=\mathrm{2}\int\frac{\mathrm{2}}{\mathrm{1}+\mathrm{3}{t}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{4}\int\frac{\mathrm{1}}{\mathrm{1}+\left(\sqrt{\mathrm{3}}{t}\right)^{\mathrm{2}} }{dt}−\mathrm{2}\int\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \sqrt{\mathrm{3}}{t}−\mathrm{2}{tan}^{−\mathrm{1}} {t}+{c} \\ $$$$=\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{3}}{tan}\frac{{x}}{\mathrm{2}}\right)−{x}+{c} \\ $$
Commented by john santu last updated on 10/Jan/20

