Question Number 12267 by tawa last updated on 17/Apr/17

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{nth}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sequence} \\ $$$$\left.\mathrm{1}\right)\:\:\:\frac{\mathrm{1}}{\mathrm{3}}\:,\:\frac{\mathrm{1}}{\mathrm{15}}\:,\:\frac{\mathrm{1}}{\mathrm{35}}\:,\:\frac{\mathrm{1}}{\mathrm{63}}\:,\:\frac{\mathrm{1}}{\mathrm{99}} \\ $$$$\left.\mathrm{2}\right)\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}},\:\frac{\mathrm{1}}{\mathrm{6}},\:\frac{\mathrm{1}}{\mathrm{12}},\:\frac{\mathrm{1}}{\mathrm{20}},\:\frac{\mathrm{1}}{\mathrm{30}} \\ $$
Answered by ajfour last updated on 17/Apr/17

$$\left.\mathrm{1}\right)\:\:{T}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:\:{T}_{{n}} =\frac{\mathrm{1}}{{n}^{\mathrm{2}} +{n}} \\ $$
Commented by tawa last updated on 17/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Joel576 last updated on 17/Apr/17
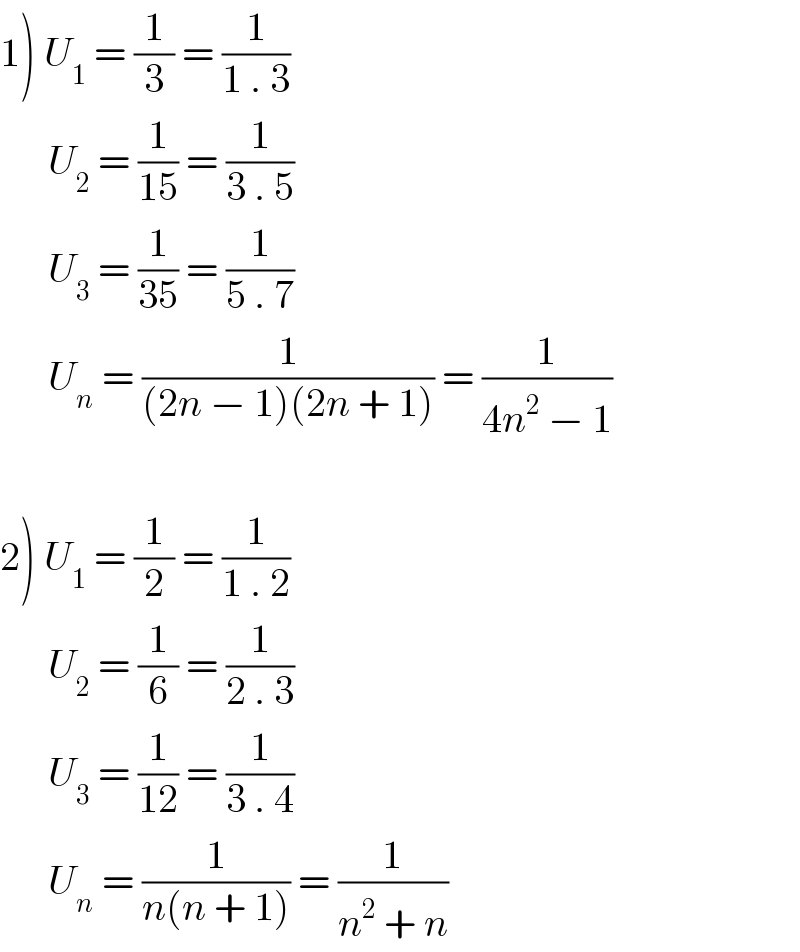
$$\left.\mathrm{1}\right)\:{U}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{1}}{\mathrm{1}\:.\:\mathrm{3}} \\ $$$$\:\:\:\:\:\:{U}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{15}}\:=\:\frac{\mathrm{1}}{\mathrm{3}\:.\:\mathrm{5}} \\ $$$$\:\:\:\:\:\:{U}_{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{35}}\:=\:\frac{\mathrm{1}}{\mathrm{5}\:.\:\mathrm{7}} \\ $$$$\:\:\:\:\:\:{U}_{{n}} \:=\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}\:−\:\mathrm{1}\right)\left(\mathrm{2}{n}\:+\:\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} \:−\:\mathrm{1}} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{U}_{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{1}\:.\:\mathrm{2}} \\ $$$$\:\:\:\:\:\:{U}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{6}}\:=\:\frac{\mathrm{1}}{\mathrm{2}\:.\:\mathrm{3}}\:\:\:\: \\ $$$$\:\:\:\:\:\:{U}_{\mathrm{3}} \:=\:\frac{\mathrm{1}}{\mathrm{12}}\:=\:\frac{\mathrm{1}}{\mathrm{3}\:.\:\mathrm{4}} \\ $$$$\:\:\:\:\:\:{U}_{{n}} \:=\:\frac{\mathrm{1}}{{n}\left({n}\:+\:\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} \:+\:{n}} \\ $$
Commented by tawa last updated on 17/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
