Question Number 77864 by Pratah last updated on 11/Jan/20
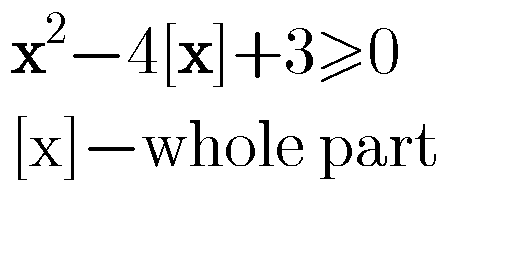
Commented by Pratah last updated on 11/Jan/20
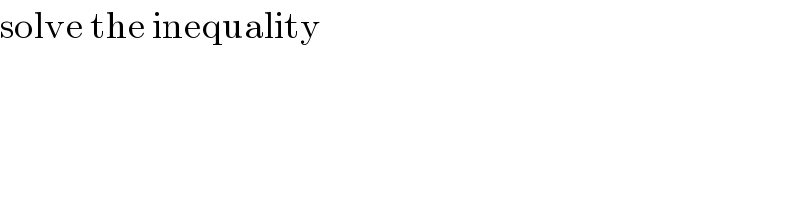
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{inequality} \\ $$
Answered by key of knowledge last updated on 11/Jan/20
![x={x}+[x]⇒ x^2 −4(x−{x})+3≥0⇒x^2 −4x+3+4{x}≥0⇒ in x≤1∨3≤x⇒x^2 −4x+3 and ∀x,4{x}≥0⇒ (−∞,1]∩[3,+∞)⇒x^2 −4[x]+3≥0(i) 1≤x<2⇒x^2 −1≥0⇒x∈R−(−1,1) ⇒1≤x<2 (ii) 2≤x<3⇒x^2 −5≥0⇒x∈R−(−(√5),(√5)) ⇒(√5)≤x<3 (iii) i∪ii∪iii⇒x∈R−[2,(√5))](https://www.tinkutara.com/question/Q77878.png)
$$\mathrm{x}=\left\{\mathrm{x}\right\}+\left[\mathrm{x}\right]\Rightarrow \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{x}−\left\{\mathrm{x}\right\}\right)+\mathrm{3}\geqslant\mathrm{0}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}+\mathrm{4}\left\{\mathrm{x}\right\}\geqslant\mathrm{0}\Rightarrow \\ $$$$\mathrm{in}\:\mathrm{x}\leqslant\mathrm{1}\vee\mathrm{3}\leqslant\mathrm{x}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{3}\:\mathrm{and}\:\forall\mathrm{x},\mathrm{4}\left\{\mathrm{x}\right\}\geqslant\mathrm{0}\Rightarrow \\ $$$$\left(−\infty,\mathrm{1}\right]\cap\left[\mathrm{3},+\infty\right)\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{4}\left[\mathrm{x}\right]+\mathrm{3}\geqslant\mathrm{0}\left({i}\right) \\ $$$$\mathrm{1}\leqslant\mathrm{x}<\mathrm{2}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{1}\geqslant\mathrm{0}\Rightarrow\mathrm{x}\in\mathrm{R}−\left(−\mathrm{1},\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{1}\leqslant\mathrm{x}<\mathrm{2}\:\:\:\left({ii}\right) \\ $$$$\mathrm{2}\leqslant\mathrm{x}<\mathrm{3}\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{5}\geqslant\mathrm{0}\Rightarrow\mathrm{x}\in\mathrm{R}−\left(−\sqrt{\mathrm{5}},\sqrt{\mathrm{5}}\right) \\ $$$$\Rightarrow\sqrt{\mathrm{5}}\leqslant\mathrm{x}<\mathrm{3}\:\:\:\left({iii}\right) \\ $$$${i}\cup{ii}\cup{iii}\Rightarrow\mathrm{x}\in\mathrm{R}−\left[\mathrm{2},\sqrt{\mathrm{5}}\right) \\ $$
