Question Number 143475 by Ghaniy last updated on 14/Jun/21
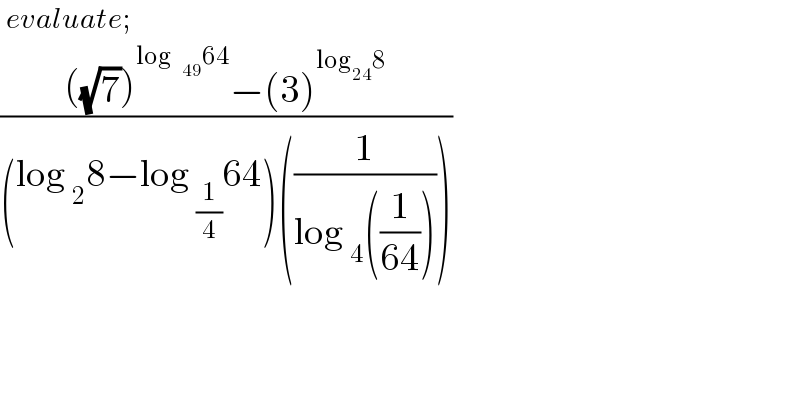
$$\:{evaluate}; \\ $$$$\frac{\left(\sqrt{\mathrm{7}}\right)^{\mathrm{log64}} −\left(\mathrm{3}\right)^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} }{\left(\mathrm{log}\:_{\mathrm{2}} \mathrm{8}−\mathrm{log}\:_{\frac{\mathrm{1}}{\mathrm{4}}} \mathrm{64}\right)\left(\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{64}}\right)}\right)} \\ $$
Commented by amin96 last updated on 14/Jun/21

$${super} \\ $$
Answered by Ar Brandon last updated on 15/Jun/21
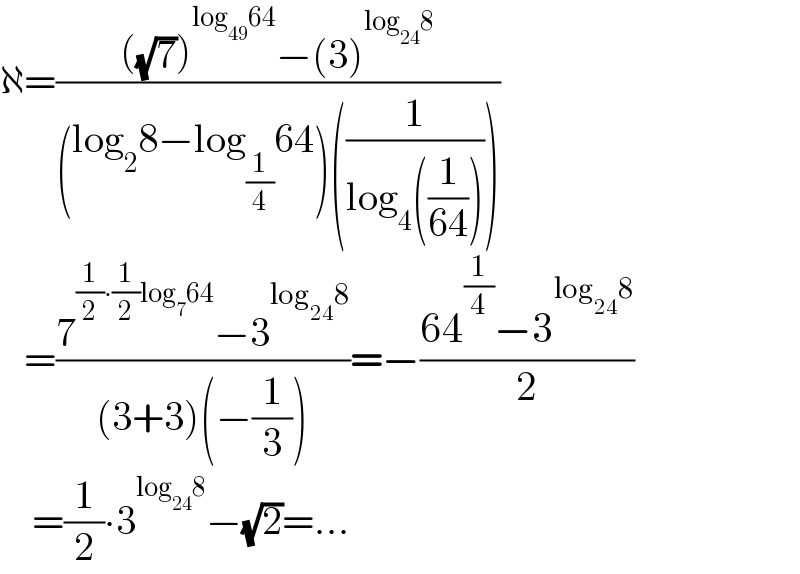
$$\aleph=\frac{\left(\sqrt{\mathrm{7}}\right)^{\mathrm{log}_{\mathrm{49}} \mathrm{64}} −\left(\mathrm{3}\right)^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} }{\left(\mathrm{log}_{\mathrm{2}} \mathrm{8}−\mathrm{log}_{\frac{\mathrm{1}}{\mathrm{4}}} \mathrm{64}\right)\left(\frac{\mathrm{1}}{\mathrm{log}_{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{64}}\right)}\right)} \\ $$$$\:\:\:=\frac{\mathrm{7}^{\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}_{\mathrm{7}} \mathrm{64}} −\mathrm{3}^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} }{\left(\mathrm{3}+\mathrm{3}\right)\left(−\frac{\mathrm{1}}{\mathrm{3}}\right)}=−\frac{\mathrm{64}^{\frac{\mathrm{1}}{\mathrm{4}}} −\mathrm{3}^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} }{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{3}^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} −\sqrt{\mathrm{2}}=… \\ $$
Commented by Ghaniy last updated on 15/Jun/21

$${thanks} \\ $$
