Question Number 12489 by Joel577 last updated on 23/Apr/17
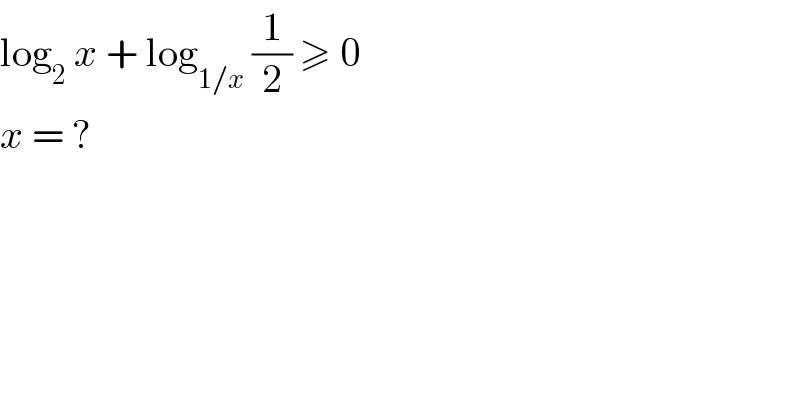
$$\mathrm{log}_{\mathrm{2}} \:{x}\:+\:\mathrm{log}_{\mathrm{1}/{x}} \:\frac{\mathrm{1}}{\mathrm{2}}\:\geqslant\:\mathrm{0} \\ $$$${x}\:=\:? \\ $$
Answered by mrW1 last updated on 23/Apr/17
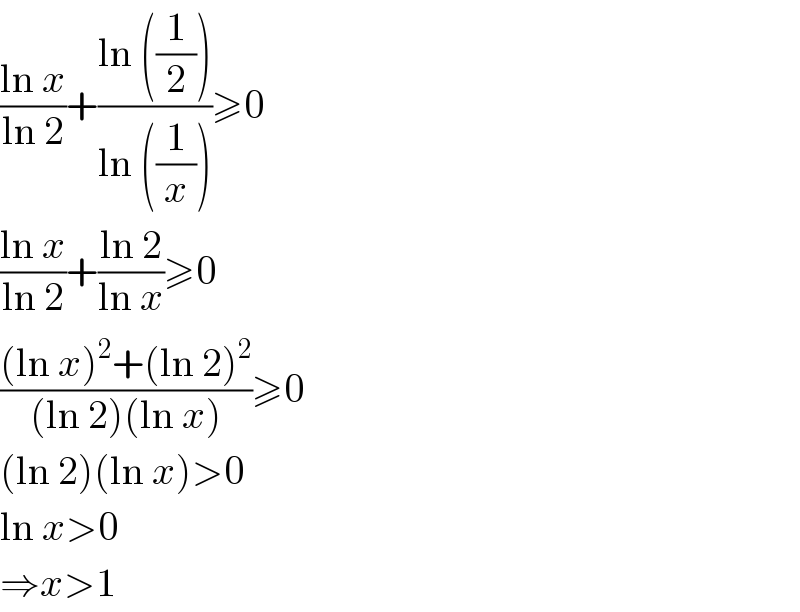
$$\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}}+\frac{\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{ln}\:\left(\frac{\mathrm{1}}{{x}}\right)}\geqslant\mathrm{0} \\ $$$$\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{2}}+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:{x}}\geqslant\mathrm{0} \\ $$$$\frac{\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} +\left(\mathrm{ln}\:\mathrm{2}\right)^{\mathrm{2}} }{\left(\mathrm{ln}\:\mathrm{2}\right)\left(\mathrm{ln}\:{x}\right)}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{ln}\:\mathrm{2}\right)\left(\mathrm{ln}\:{x}\right)>\mathrm{0} \\ $$$$\mathrm{ln}\:{x}>\mathrm{0} \\ $$$$\Rightarrow{x}>\mathrm{1} \\ $$
Commented by Joel577 last updated on 24/Apr/17
$${thank}\:{you}\:{very}\:{much} \\ $$
