Question Number 143588 by bobhans last updated on 16/Jun/21
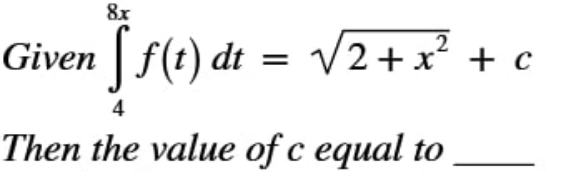
Answered by EDWIN88 last updated on 16/Jun/21
![F(x)=∫_4 ^(8x) f(t) dt = (√(2+x^2 )) + c F ′(x)= 8f(8x)=(x/( (√(2+x^2 )))) F′(x)=f(8x)=(x/(8(√(2+x^2 )))) ⇒f(x)=(((1/8)x)/(8(√(2+(1/(64))x^2 )))) = (x/(8(√(128+x^2 )))) ⇒f(t)=(t/(8(√(128+t^2 )))) F(x)=∫_4 ^(8x) [(t/(8(√(128+t^2 )))) ]dt = (√(2+x^2 )) +c take x=(1/2) ⇒F((1/2))=∫_( 4) ^(8.(1/2)) [(t/(8(√(128+t^2 )))) ]dt =(√(2+(1/4))) +c ⇒ 0 = (3/2)+c ; c =−(3/2)](https://www.tinkutara.com/question/Q143590.png)
$$\mathrm{F}\left(\mathrm{x}\right)=\underset{\mathrm{4}} {\overset{\mathrm{8x}} {\int}}\:\mathrm{f}\left(\mathrm{t}\right)\:\mathrm{dt}\:=\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{c}\: \\ $$$$\mathrm{F}\:'\left(\mathrm{x}\right)=\:\mathrm{8f}\left(\mathrm{8x}\right)=\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }}\: \\ $$$$\mathrm{F}'\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{8x}\right)=\frac{\mathrm{x}}{\mathrm{8}\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\frac{\mathrm{1}}{\mathrm{8}}\mathrm{x}}{\mathrm{8}\sqrt{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{64}}\mathrm{x}^{\mathrm{2}} }}\:=\:\frac{\mathrm{x}}{\mathrm{8}\sqrt{\mathrm{128}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\mathrm{8}\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }} \\ $$$$\mathrm{F}\left(\mathrm{x}\right)=\underset{\mathrm{4}} {\overset{\mathrm{8x}} {\int}}\:\left[\frac{\mathrm{t}}{\mathrm{8}\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }}\:\right]\mathrm{dt}\:=\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{c} \\ $$$$\mathrm{take}\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{F}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\underset{\:\mathrm{4}} {\overset{\mathrm{8}.\frac{\mathrm{1}}{\mathrm{2}}} {\int}}\left[\frac{\mathrm{t}}{\mathrm{8}\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }}\:\right]\mathrm{dt}\:=\sqrt{\mathrm{2}+\frac{\mathrm{1}}{\mathrm{4}}}\:+\mathrm{c} \\ $$$$\Rightarrow\:\mathrm{0}\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{c}\:;\:\mathrm{c}\:=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 16/Jun/21
![∫_4 ^(8x) f(t)dt=(√(2+x^2 )) +c by derivation we get 8f(8x)=((2x)/(2(√(2+x^2 ))))=(x/( (√(2+x^2 )))) ⇒f(8x)=(x/(8(√(2+x^2 )))) 8x=t ⇒f(t)=(t/(64(√(2+(t^2 /8^2 ))))) =(t/(8(√(128+t^2 )))) x=0 ⇒−∫_0 ^4 f(t)dt=(√2)+c ⇒c=−(√2)−∫_0 ^4 f(t)dt =−(√2)−(1/8)∫_0 ^4 (t/( (√(128+t^2 ))))dt =−(√2)[(√(128+t^2 ))]_0 ^4 =−(√2)((√(128+16))−(√(128)))=−(√2)((√(144))−(√(128)))](https://www.tinkutara.com/question/Q143619.png)
$$\int_{\mathrm{4}} ^{\mathrm{8x}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }\:+\mathrm{c}\:\:\mathrm{by}\:\mathrm{derivation}\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{8f}\left(\mathrm{8x}\right)=\frac{\mathrm{2x}}{\mathrm{2}\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }}=\frac{\mathrm{x}}{\:\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }}\:\Rightarrow\mathrm{f}\left(\mathrm{8x}\right)=\frac{\mathrm{x}}{\mathrm{8}\sqrt{\mathrm{2}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{8x}=\mathrm{t}\:\Rightarrow\mathrm{f}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\mathrm{64}\sqrt{\mathrm{2}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{8}^{\mathrm{2}} }}}\:=\frac{\mathrm{t}}{\mathrm{8}\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }} \\ $$$$\mathrm{x}=\mathrm{0}\:\Rightarrow−\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt}=\sqrt{\mathrm{2}}+\mathrm{c}\:\Rightarrow\mathrm{c}=−\sqrt{\mathrm{2}}−\int_{\mathrm{0}} ^{\mathrm{4}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=−\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{4}} \:\:\frac{\mathrm{t}}{\:\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }}\mathrm{dt}\:=−\sqrt{\mathrm{2}}\left[\sqrt{\mathrm{128}+\mathrm{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=−\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{128}+\mathrm{16}}−\sqrt{\mathrm{128}}\right)=−\sqrt{\mathrm{2}}\left(\sqrt{\mathrm{144}}−\sqrt{\mathrm{128}}\right) \\ $$
Answered by mindispower last updated on 16/Jun/21
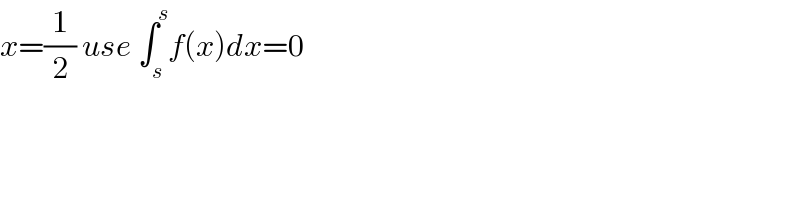
$${x}=\frac{\mathrm{1}}{\mathrm{2}}\:{use}\:\int_{{s}} ^{{s}} {f}\left({x}\right){dx}=\mathrm{0} \\ $$
