Menu Close

Question-143627

Tinku Tara 0 Comments
Pin




Question Number 143627 by bobhans last updated on 16/Jun/21
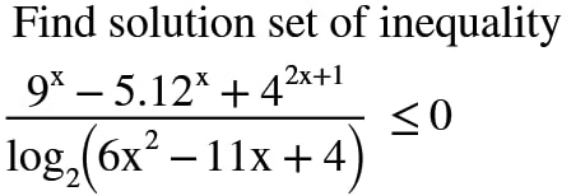
Answered by Olaf_Thorendsen last updated on 16/Jun/21
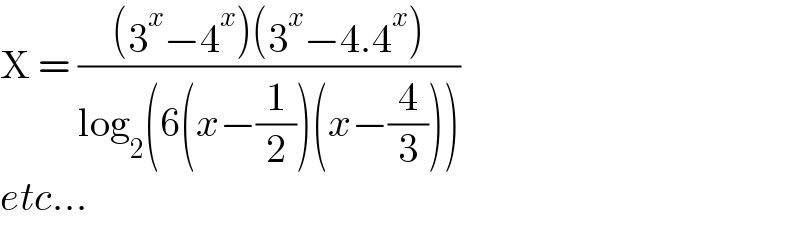
X = (((3^x −4^x )(3^x −4.4^x ))/(log_2 (6(x−(1/2))(x−(4/3))))) etc...
$$\mathrm{X}\:=\:\frac{\left(\mathrm{3}^{{x}} −\mathrm{4}^{{x}} \right)\left(\mathrm{3}^{{x}} −\mathrm{4}.\mathrm{4}^{{x}} \right)}{\mathrm{log}_{\mathrm{2}} \left(\mathrm{6}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{4}}{\mathrm{3}}\right)\right)} \\ $$$${etc}… \\ $$
Answered by Canebulok last updated on 18/Jun/21
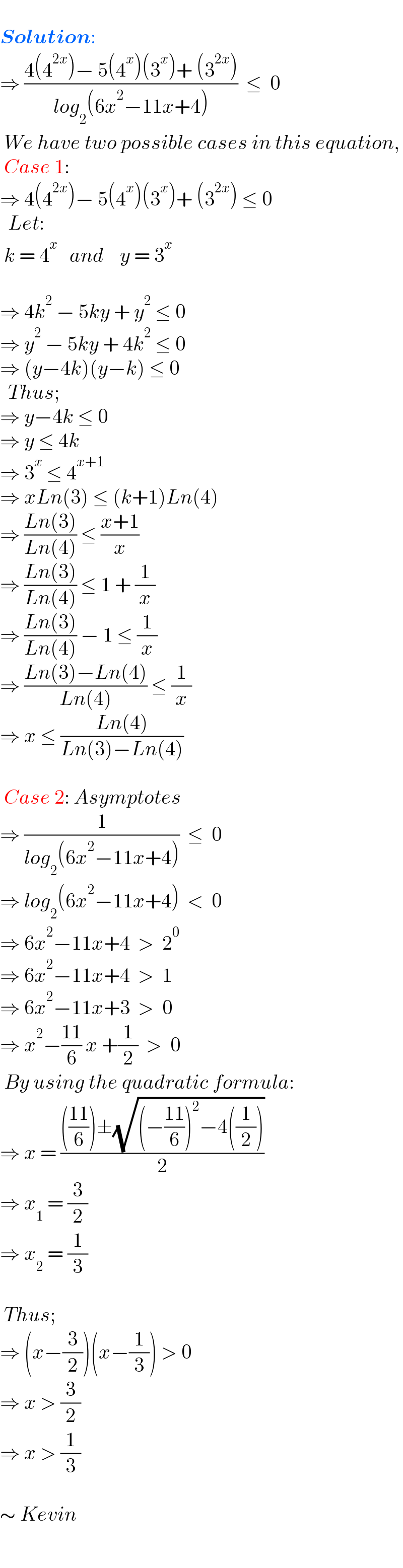
Solution: ⇒ ((4(4^(2x) )− 5(4^x )(3^x )+ (3^(2x) ))/(log_2 (6x^2 −11x+4))) ≤ 0 We have two possible cases in this equation, Case 1: ⇒ 4(4^(2x) )− 5(4^x )(3^x )+ (3^(2x) ) ≤ 0 Let: k = 4^x and y = 3^x ⇒ 4k^2 − 5ky + y^2 ≤ 0 ⇒ y^2 − 5ky + 4k^2 ≤ 0 ⇒ (y−4k)(y−k) ≤ 0 Thus; ⇒ y−4k ≤ 0 ⇒ y ≤ 4k ⇒ 3^x ≤ 4^(x+1) ⇒ xLn(3) ≤ (k+1)Ln(4) ⇒ ((Ln(3))/(Ln(4))) ≤ ((x+1)/x) ⇒ ((Ln(3))/(Ln(4))) ≤ 1 + (1/x) ⇒ ((Ln(3))/(Ln(4))) − 1 ≤ (1/x) ⇒ ((Ln(3)−Ln(4))/(Ln(4))) ≤ (1/x) ⇒ x ≤ ((Ln(4))/(Ln(3)−Ln(4))) Case 2: Asymptotes ⇒ (1/(log_2 (6x^2 −11x+4))) ≤ 0 ⇒ log_2 (6x^2 −11x+4) < 0 ⇒ 6x^2 −11x+4 > 2^0 ⇒ 6x^2 −11x+4 > 1 ⇒ 6x^2 −11x+3 > 0 ⇒ x^2 −((11)/6) x +(1/2) > 0 By using the quadratic formula: ⇒ x = (((((11)/6))±(√((−((11)/6))^2 −4((1/2)))))/2) ⇒ x_1 = (3/2) ⇒ x_2 = (1/3) Thus; ⇒ (x−(3/2))(x−(1/3)) > 0 ⇒ x > (3/2) ⇒ x > (1/3) ∼ Kevin
$$\: \\ $$$$\boldsymbol{{Solution}}: \\ $$$$\Rightarrow\:\frac{\mathrm{4}\left(\mathrm{4}^{\mathrm{2}{x}} \right)−\:\mathrm{5}\left(\mathrm{4}^{{x}} \right)\left(\mathrm{3}^{{x}} \right)+\:\left(\mathrm{3}^{\mathrm{2}{x}} \right)}{{log}_{\mathrm{2}} \left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{4}\right)}\:\:\leq\:\:\mathrm{0} \\ $$$$\:{We}\:{have}\:{two}\:{possible}\:{cases}\:{in}\:{this}\:{equation}, \\ $$$$\:{Case}\:\mathrm{1}: \\ $$$$\Rightarrow\:\mathrm{4}\left(\mathrm{4}^{\mathrm{2}{x}} \right)−\:\mathrm{5}\left(\mathrm{4}^{{x}} \right)\left(\mathrm{3}^{{x}} \right)+\:\left(\mathrm{3}^{\mathrm{2}{x}} \right)\:\leq\:\mathrm{0} \\ $$$$\:\:{Let}: \\ $$$$\:{k}\:=\:\mathrm{4}^{{x}} \:\:\:{and}\:\:\:\:{y}\:=\:\mathrm{3}^{{x}} \\ $$$$\: \\ $$$$\Rightarrow\:\mathrm{4}{k}^{\mathrm{2}} \:−\:\mathrm{5}{ky}\:+\:{y}^{\mathrm{2}} \:\leq\:\mathrm{0} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} \:−\:\mathrm{5}{ky}\:+\:\mathrm{4}{k}^{\mathrm{2}} \:\leq\:\mathrm{0} \\ $$$$\Rightarrow\:\left({y}−\mathrm{4}{k}\right)\left({y}−{k}\right)\:\leq\:\mathrm{0} \\ $$$$\:\:{Thus}; \\ $$$$\Rightarrow\:{y}−\mathrm{4}{k}\:\leq\:\mathrm{0} \\ $$$$\Rightarrow\:{y}\:\leq\:\mathrm{4}{k} \\ $$$$\Rightarrow\:\mathrm{3}^{{x}} \:\leq\:\mathrm{4}^{{x}+\mathrm{1}} \\ $$$$\Rightarrow\:{xLn}\left(\mathrm{3}\right)\:\leq\:\left({k}+\mathrm{1}\right){Ln}\left(\mathrm{4}\right) \\ $$$$\Rightarrow\:\frac{{Ln}\left(\mathrm{3}\right)}{{Ln}\left(\mathrm{4}\right)}\:\leq\:\frac{{x}+\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:\frac{{Ln}\left(\mathrm{3}\right)}{{Ln}\left(\mathrm{4}\right)}\:\leq\:\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:\frac{{Ln}\left(\mathrm{3}\right)}{{Ln}\left(\mathrm{4}\right)}\:−\:\mathrm{1}\:\leq\:\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:\frac{{Ln}\left(\mathrm{3}\right)−{Ln}\left(\mathrm{4}\right)}{{Ln}\left(\mathrm{4}\right)}\:\leq\:\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\:{x}\:\leq\:\frac{{Ln}\left(\mathrm{4}\right)}{{Ln}\left(\mathrm{3}\right)−{Ln}\left(\mathrm{4}\right)} \\ $$$$\: \\ $$$$\:{Case}\:\mathrm{2}:\:{Asymptotes} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{log}_{\mathrm{2}} \left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{4}\right)}\:\:\leq\:\:\mathrm{0} \\ $$$$\Rightarrow\:{log}_{\mathrm{2}} \left(\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{4}\right)\:\:<\:\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{4}\:\:>\:\:\mathrm{2}^{\mathrm{0}} \\ $$$$\Rightarrow\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{4}\:\:>\:\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{6}{x}^{\mathrm{2}} −\mathrm{11}{x}+\mathrm{3}\:\:>\:\:\mathrm{0} \\ $$$$\Rightarrow\:{x}^{\mathrm{2}} −\frac{\mathrm{11}}{\mathrm{6}}\:{x}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\:>\:\:\mathrm{0} \\ $$$$\:{By}\:{using}\:{the}\:{quadratic}\:{formula}: \\ $$$$\Rightarrow\:{x}\:=\:\frac{\left(\frac{\mathrm{11}}{\mathrm{6}}\right)\pm\sqrt{\left(−\frac{\mathrm{11}}{\mathrm{6}}\right)^{\mathrm{2}} −\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} \:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}_{\mathrm{2}} \:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\: \\ $$$$\:{Thus}; \\ $$$$\Rightarrow\:\left({x}−\frac{\mathrm{3}}{\mathrm{2}}\right)\left({x}−\frac{\mathrm{1}}{\mathrm{3}}\right)\:>\:\mathrm{0} \\ $$$$\Rightarrow\:{x}\:>\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}\:>\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\: \\ $$$$\sim\:{Kevin} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *