Menu Close

Question-143677

Tinku Tara 0 Comments
Pin




Question Number 143677 by bobhans last updated on 17/Jun/21
Answered by bemath last updated on 17/Jun/21
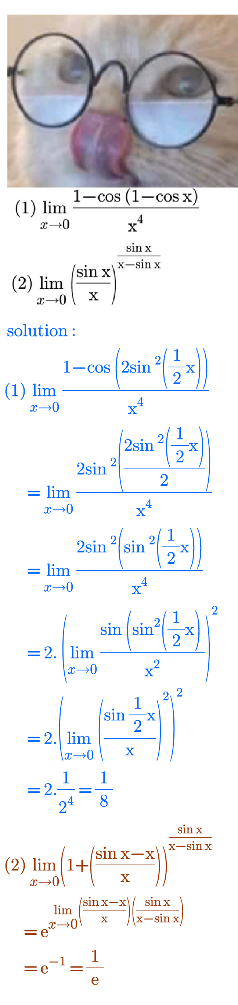
Answered by mathmax by abdo last updated on 17/Jun/21
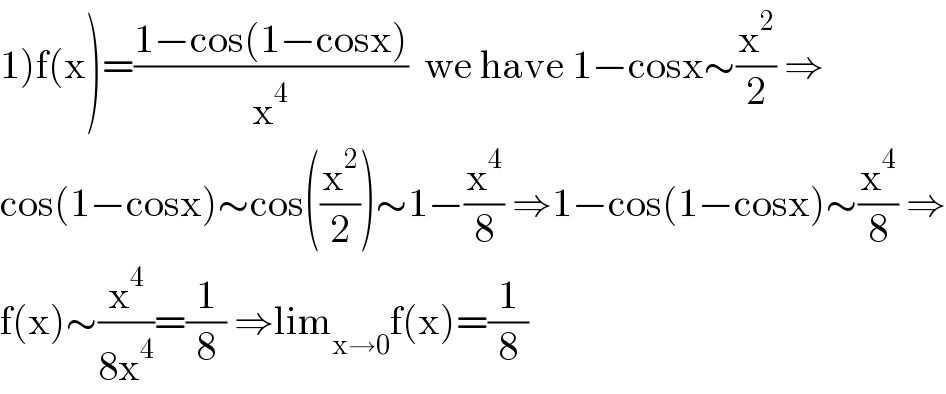
1)f(x)=((1−cos(1−cosx))/x^4 ) we have 1−cosx∼(x^2 /2) ⇒ cos(1−cosx)∼cos((x^2 /2))∼1−(x^4 /8) ⇒1−cos(1−cosx)∼(x^4 /8) ⇒ f(x)∼(x^4 /(8x^4 ))=(1/8) ⇒lim_(x→0) f(x)=(1/8)
$$\left.\mathrm{1}\right)\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{1}−\mathrm{cosx}\right)}{\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}−\mathrm{cosx}\sim\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{cos}\left(\mathrm{1}−\mathrm{cosx}\right)\sim\mathrm{cos}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{8}}\:\Rightarrow\mathrm{1}−\mathrm{cos}\left(\mathrm{1}−\mathrm{cosx}\right)\sim\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\sim\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{8x}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Answered by mathmax by abdo last updated on 17/Jun/21
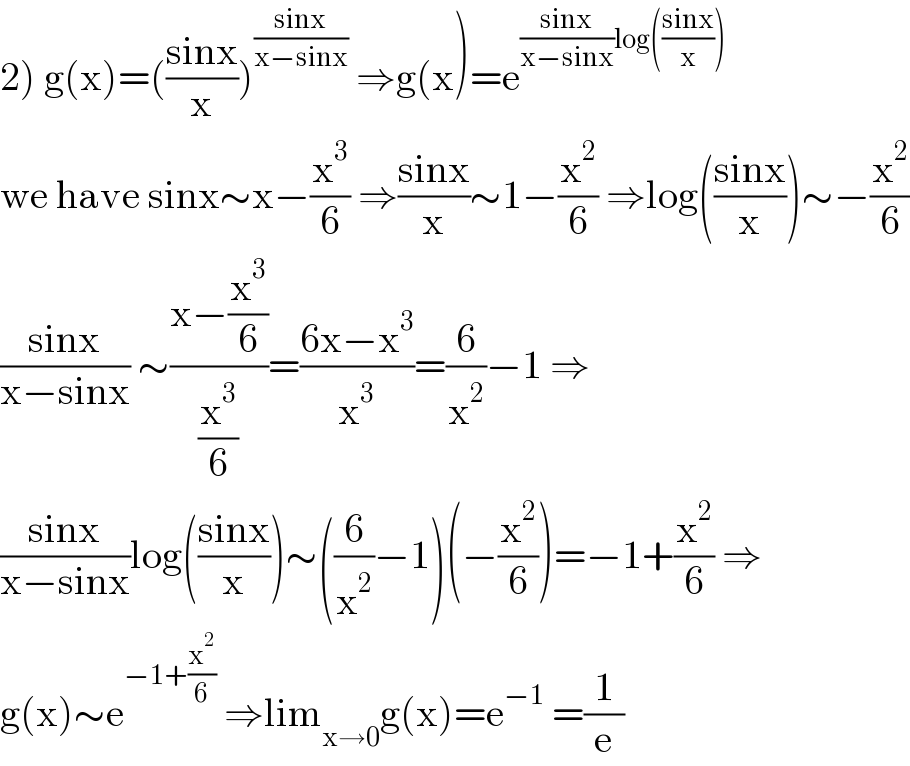
2) g(x)=(((sinx)/x))^((sinx)/(x−sinx)) ⇒g(x)=e^(((sinx)/(x−sinx))log(((sinx)/x))) we have sinx∼x−(x^3 /6) ⇒((sinx)/x)∼1−(x^2 /6) ⇒log(((sinx)/x))∼−(x^2 /6) ((sinx)/(x−sinx)) ∼((x−(x^3 /6))/(x^3 /6))=((6x−x^3 )/x^3 )=(6/x^2 )−1 ⇒ ((sinx)/(x−sinx))log(((sinx)/x))∼((6/x^2 )−1)(−(x^2 /6))=−1+(x^2 /6) ⇒ g(x)∼e^(−1+(x^2 /6)) ⇒lim_(x→0) g(x)=e^(−1) =(1/e)
$$\left.\mathrm{2}\right)\:\mathrm{g}\left(\mathrm{x}\right)=\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\frac{\mathrm{sinx}}{\mathrm{x}−\mathrm{sinx}}} \:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)=\mathrm{e}^{\frac{\mathrm{sinx}}{\mathrm{x}−\mathrm{sinx}}\mathrm{log}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{sinx}\sim\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow\frac{\mathrm{sinx}}{\mathrm{x}}\sim\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow\mathrm{log}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\sim−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\frac{\mathrm{sinx}}{\mathrm{x}−\mathrm{sinx}}\:\sim\frac{\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}{\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}}=\frac{\mathrm{6x}−\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{6}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\:\Rightarrow \\ $$$$\frac{\mathrm{sinx}}{\mathrm{x}−\mathrm{sinx}}\mathrm{log}\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)\sim\left(\frac{\mathrm{6}}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\right)\left(−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\right)=−\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}\:\Rightarrow \\ $$$$\mathrm{g}\left(\mathrm{x}\right)\sim\mathrm{e}^{−\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{6}}} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{1}} \:=\frac{\mathrm{1}}{\mathrm{e}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *