Question Number 1041 by tera last updated on 22/May/15
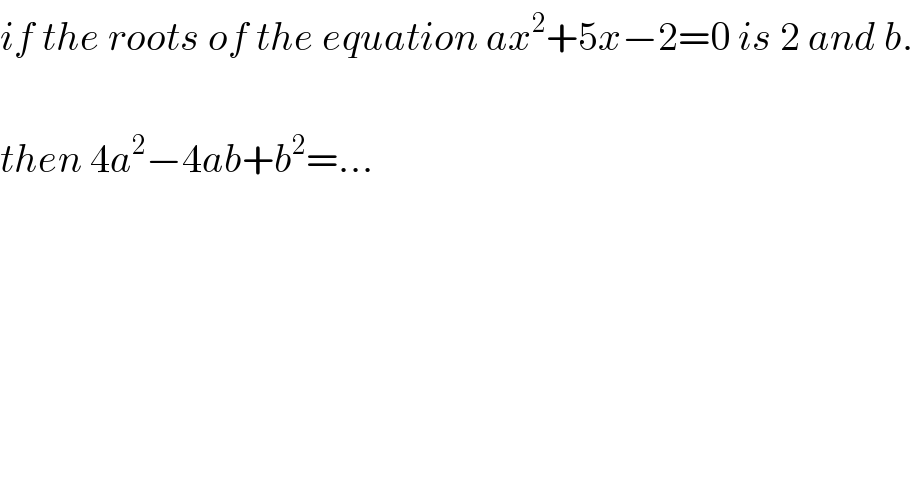
$${if}\:{the}\:{roots}\:{of}\:{the}\:{equation}\:{ax}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2}=\mathrm{0}\:{is}\:\mathrm{2}\:{and}\:{b}. \\ $$$$ \\ $$$${then}\:\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}+{b}^{\mathrm{2}} =… \\ $$
Answered by prakash jain last updated on 23/May/15
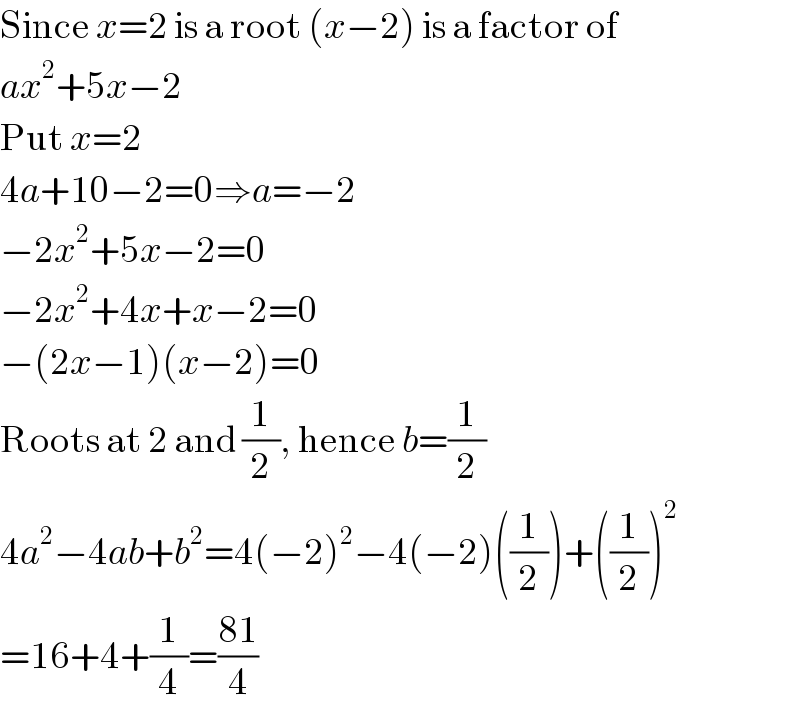
$$\mathrm{Since}\:{x}=\mathrm{2}\:\mathrm{is}\:\mathrm{a}\:\mathrm{root}\:\left({x}−\mathrm{2}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{factor}\:\mathrm{of} \\ $$$${ax}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2} \\ $$$$\mathrm{Put}\:{x}=\mathrm{2} \\ $$$$\mathrm{4}{a}+\mathrm{10}−\mathrm{2}=\mathrm{0}\Rightarrow{a}=−\mathrm{2} \\ $$$$−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}−\mathrm{2}=\mathrm{0} \\ $$$$−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+{x}−\mathrm{2}=\mathrm{0} \\ $$$$−\left(\mathrm{2}{x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{Roots}\:\mathrm{at}\:\mathrm{2}\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{hence}\:{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}+{b}^{\mathrm{2}} =\mathrm{4}\left(−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{4}\left(−\mathrm{2}\right)\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{16}+\mathrm{4}+\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{81}}{\mathrm{4}} \\ $$
Commented by tera last updated on 23/May/15

$${thank}\:{you}\:{sir} \\ $$
Answered by prakash jain last updated on 22/May/15
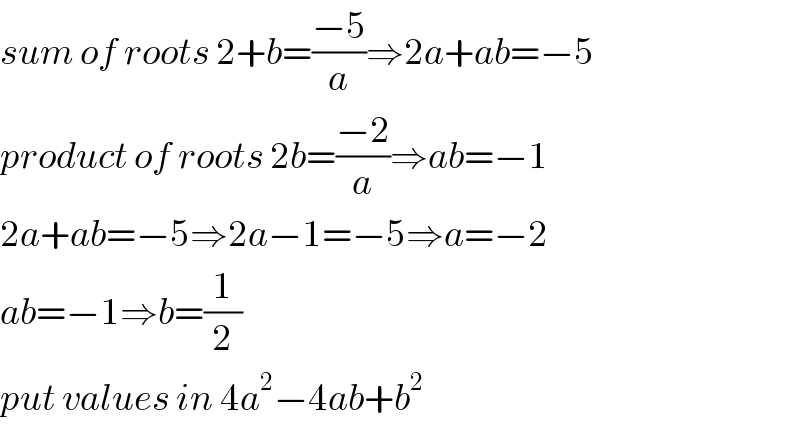
$${sum}\:{of}\:{roots}\:\mathrm{2}+{b}=\frac{−\mathrm{5}}{{a}}\Rightarrow\mathrm{2}{a}+{ab}=−\mathrm{5} \\ $$$${product}\:{of}\:{roots}\:\mathrm{2}{b}=\frac{−\mathrm{2}}{{a}}\Rightarrow{ab}=−\mathrm{1} \\ $$$$\mathrm{2}{a}+{ab}=−\mathrm{5}\Rightarrow\mathrm{2}{a}−\mathrm{1}=−\mathrm{5}\Rightarrow{a}=−\mathrm{2} \\ $$$${ab}=−\mathrm{1}\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${put}\:{values}\:{in}\:\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}+{b}^{\mathrm{2}} \\ $$
