Question Number 143726 by mathdanisur last updated on 17/Jun/21
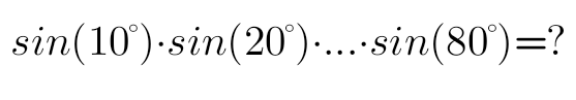
Commented by mr W last updated on 17/Jun/21

$$=\frac{\mathrm{3}}{\mathrm{256}}\:? \\ $$
Commented by mathdanisur last updated on 17/Jun/21
$${yes}\:{dear}\:{Sir}\:{solution}\:{possible}\:{please}.. \\ $$
Answered by mr W last updated on 17/Jun/21
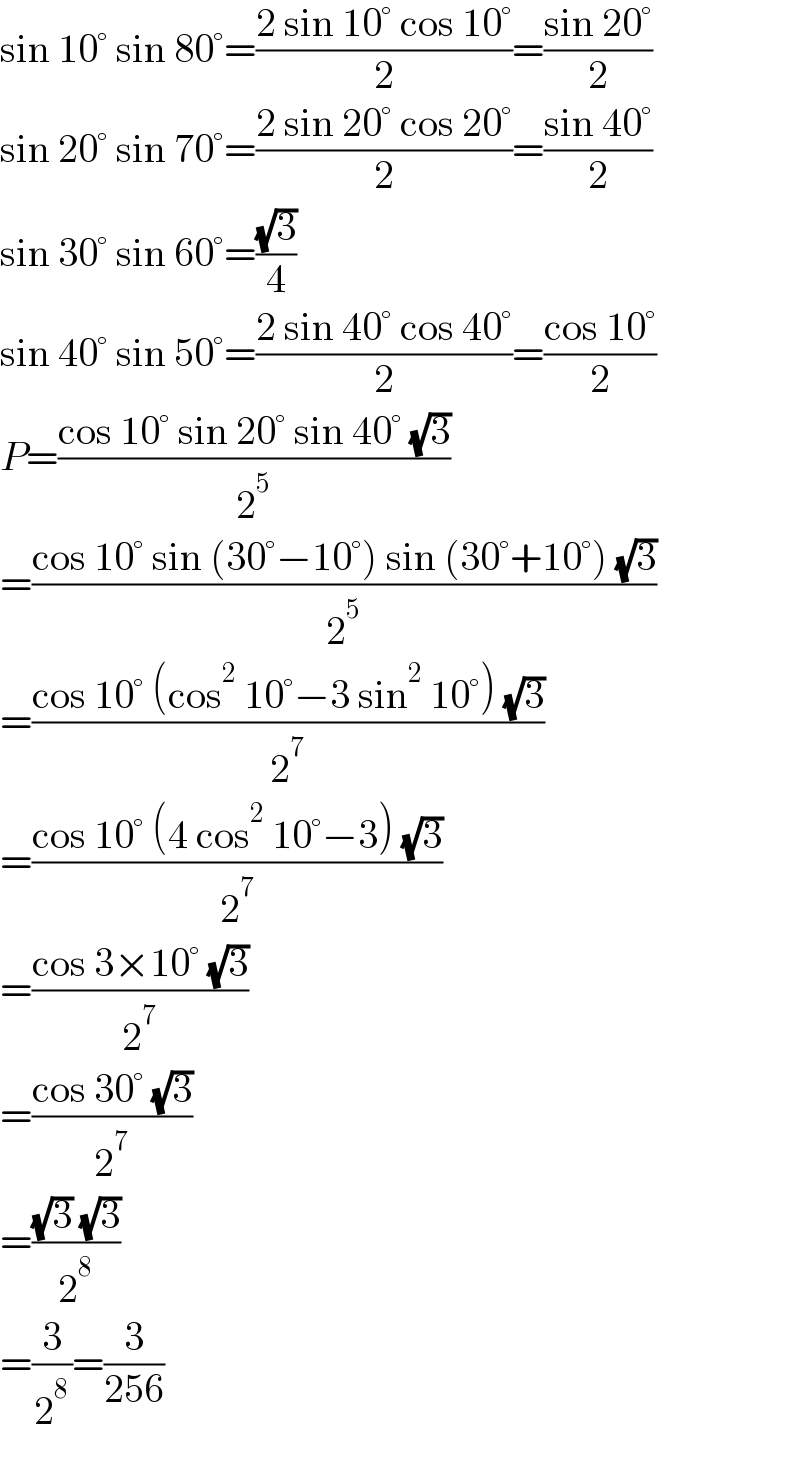
$$\mathrm{sin}\:\mathrm{10}°\:\mathrm{sin}\:\mathrm{80}°=\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{10}°\:\mathrm{cos}\:\mathrm{10}°}{\mathrm{2}}=\frac{\mathrm{sin}\:\mathrm{20}°}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{20}°\:\mathrm{sin}\:\mathrm{70}°=\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{20}°\:\mathrm{cos}\:\mathrm{20}°}{\mathrm{2}}=\frac{\mathrm{sin}\:\mathrm{40}°}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\mathrm{30}°\:\mathrm{sin}\:\mathrm{60}°=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{40}°\:\mathrm{sin}\:\mathrm{50}°=\frac{\mathrm{2}\:\mathrm{sin}\:\mathrm{40}°\:\mathrm{cos}\:\mathrm{40}°}{\mathrm{2}}=\frac{\mathrm{cos}\:\mathrm{10}°}{\mathrm{2}} \\ $$$${P}=\frac{\mathrm{cos}\:\mathrm{10}°\:\mathrm{sin}\:\mathrm{20}°\:\mathrm{sin}\:\mathrm{40}°\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{cos}\:\mathrm{10}°\:\mathrm{sin}\:\left(\mathrm{30}°−\mathrm{10}°\right)\:\mathrm{sin}\:\left(\mathrm{30}°+\mathrm{10}°\right)\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{5}} } \\ $$$$=\frac{\mathrm{cos}\:\mathrm{10}°\:\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{10}°−\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{10}°\right)\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$=\frac{\mathrm{cos}\:\mathrm{10}°\:\left(\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{10}°−\mathrm{3}\right)\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$=\frac{\mathrm{cos}\:\mathrm{3}×\mathrm{10}°\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$=\frac{\mathrm{cos}\:\mathrm{30}°\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{7}} } \\ $$$$=\frac{\sqrt{\mathrm{3}}\:\sqrt{\mathrm{3}}}{\mathrm{2}^{\mathrm{8}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{8}} }=\frac{\mathrm{3}}{\mathrm{256}} \\ $$
Commented by mathdanisur last updated on 17/Jun/21
$${perfect}\:{dear}\:{Sir},\:{thank}\:{you}\:{so}\:{much}.. \\ $$
