Question Number 143811 by liberty last updated on 18/Jun/21
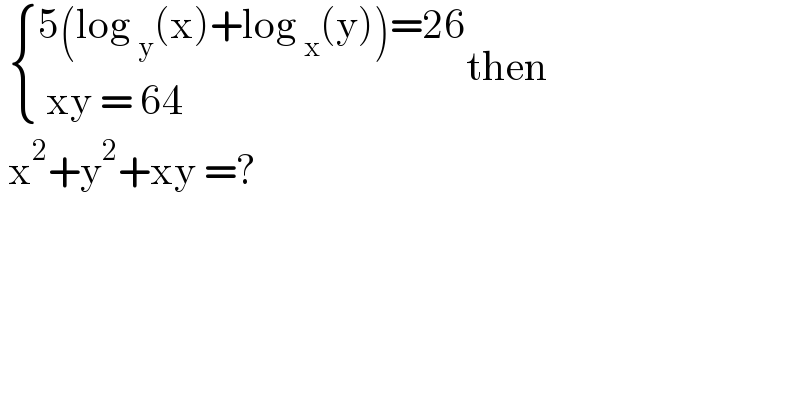
$$\:\begin{cases}{\mathrm{5}\left(\mathrm{log}\:_{\mathrm{y}} \left(\mathrm{x}\right)+\mathrm{log}\:_{\mathrm{x}} \left(\mathrm{y}\right)\right)=\mathrm{26}}\\{\:\mathrm{xy}\:=\:\mathrm{64}}\end{cases}\mathrm{then} \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy}\:=? \\ $$
Answered by liberty last updated on 18/Jun/21
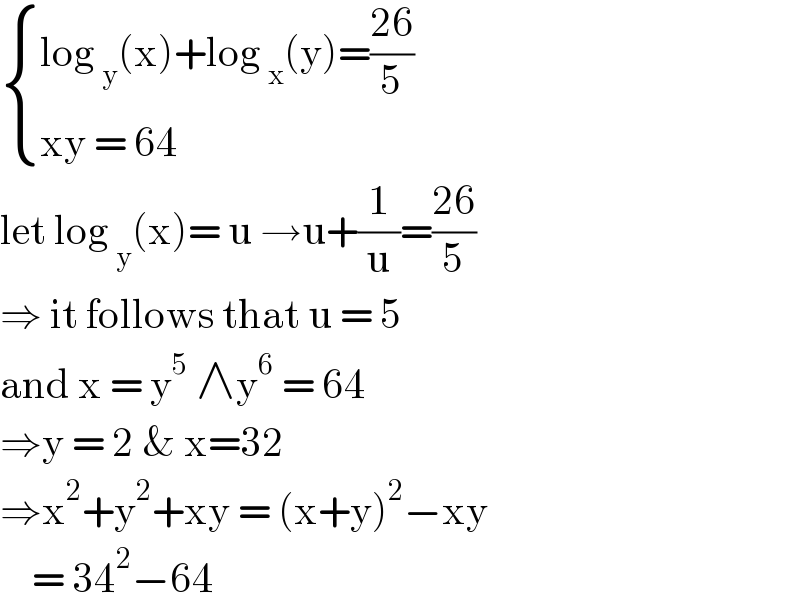
$$\begin{cases}{\mathrm{log}\:_{\mathrm{y}} \left(\mathrm{x}\right)+\mathrm{log}\:_{\mathrm{x}} \left(\mathrm{y}\right)=\frac{\mathrm{26}}{\mathrm{5}}}\\{\mathrm{xy}\:=\:\mathrm{64}\:}\end{cases} \\ $$$$\mathrm{let}\:\mathrm{log}\:_{\mathrm{y}} \left(\mathrm{x}\right)=\:\mathrm{u}\:\rightarrow\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}=\frac{\mathrm{26}}{\mathrm{5}} \\ $$$$\Rightarrow\:\mathrm{it}\:\mathrm{follows}\:\mathrm{that}\:\mathrm{u}\:=\:\mathrm{5}\: \\ $$$$\mathrm{and}\:\mathrm{x}\:=\:\mathrm{y}^{\mathrm{5}} \:\wedge\mathrm{y}^{\mathrm{6}} \:=\:\mathrm{64}\: \\ $$$$\Rightarrow\mathrm{y}\:=\:\mathrm{2}\:\&\:\mathrm{x}=\mathrm{32}\: \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{xy}\:=\:\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{2}} −\mathrm{xy} \\ $$$$\:\:\:\:=\:\mathrm{34}^{\mathrm{2}} −\mathrm{64}\: \\ $$
