Question Number 12743 by tawa last updated on 30/Apr/17

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{eqilateral}\:\mathrm{triangle}\:\mathrm{whose}\:\mathrm{inscribed}\:\mathrm{circle}\:\mathrm{has}\:\mathrm{a}\:\mathrm{radius}\:\mathrm{2} \\ $$
Answered by mrW1 last updated on 30/Apr/17
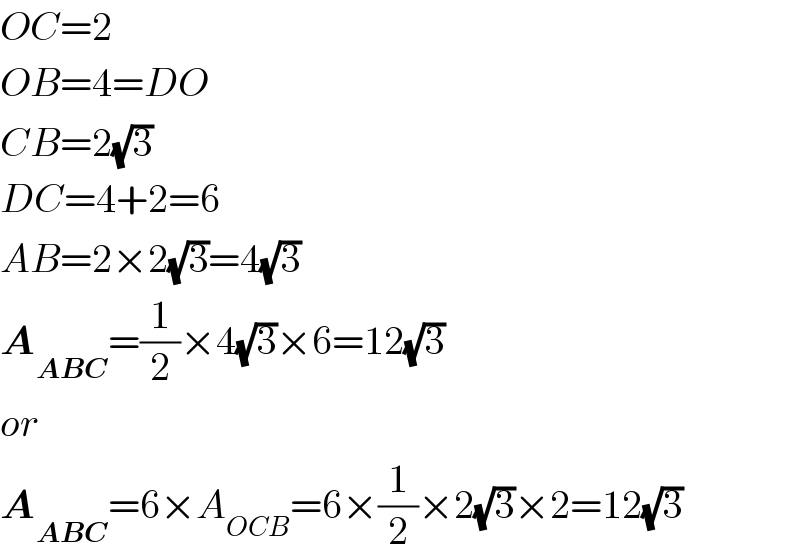
$${OC}=\mathrm{2} \\ $$$${OB}=\mathrm{4}={DO} \\ $$$${CB}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${DC}=\mathrm{4}+\mathrm{2}=\mathrm{6} \\ $$$${AB}=\mathrm{2}×\mathrm{2}\sqrt{\mathrm{3}}=\mathrm{4}\sqrt{\mathrm{3}} \\ $$$$\boldsymbol{{A}}_{\boldsymbol{{ABC}}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}\sqrt{\mathrm{3}}×\mathrm{6}=\mathrm{12}\sqrt{\mathrm{3}} \\ $$$${or} \\ $$$$\boldsymbol{{A}}_{\boldsymbol{{ABC}}} =\mathrm{6}×{A}_{{OCB}} =\mathrm{6}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}\sqrt{\mathrm{3}}×\mathrm{2}=\mathrm{12}\sqrt{\mathrm{3}} \\ $$
Commented by mrW1 last updated on 30/Apr/17
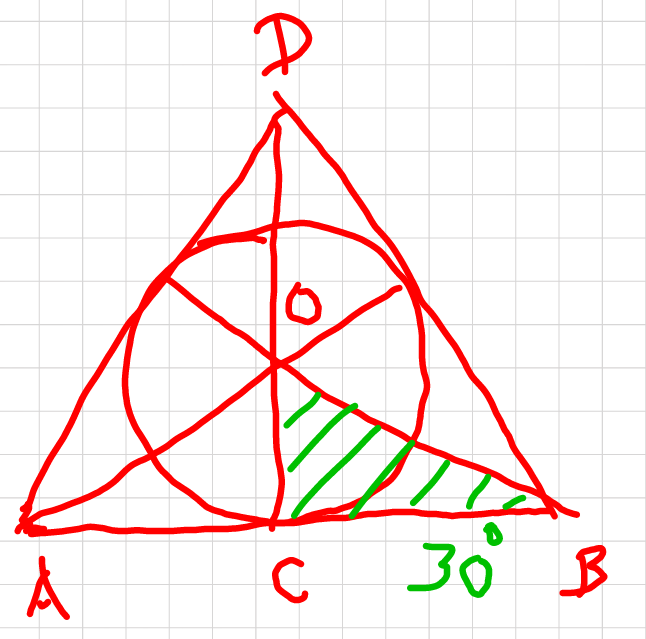
Commented by tawa last updated on 30/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/Apr/17
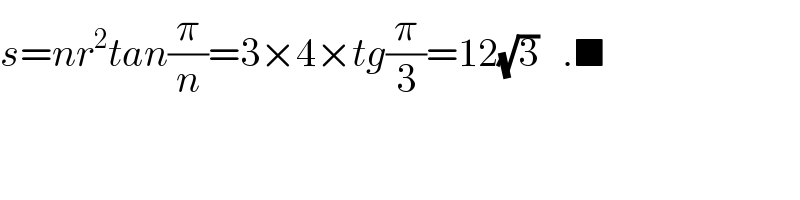
$${s}={nr}^{\mathrm{2}} {tan}\frac{\pi}{{n}}=\mathrm{3}×\mathrm{4}×{tg}\frac{\pi}{\mathrm{3}}=\mathrm{12}\sqrt{\mathrm{3}}\:\:\:.\blacksquare \\ $$
Commented by tawa last updated on 30/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
