Question Number 78316 by mathocean1 last updated on 15/Jan/20

$$\mathrm{the}\:\mathrm{circle}\:\mathrm{represents}\:\mathrm{a}\:\mathrm{farm}\:\mathrm{where} \\ $$$$\left(\mathrm{LK}\right)\:\mathrm{is}\:\mathrm{symetric}\:\mathrm{axe}\:\mathrm{of}\:\mathrm{circle}\:\mathrm{such} \\ $$$$\mathrm{as}\:\forall\:\mathrm{M}\:\mathrm{of}\:\mathrm{this}\:\mathrm{circle}\:\mathrm{verifying} \\ $$$$\mathrm{ML}^{\mathrm{2}} −\mathrm{4MK}^{\mathrm{2}} =\mathrm{0}\:\:\mathrm{with}\:\mathrm{LK}=\mathrm{150m}. \\ $$$$\mathrm{calculate}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{circle}. \\ $$$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}… \\ $$
Commented by mathocean1 last updated on 15/Jan/20
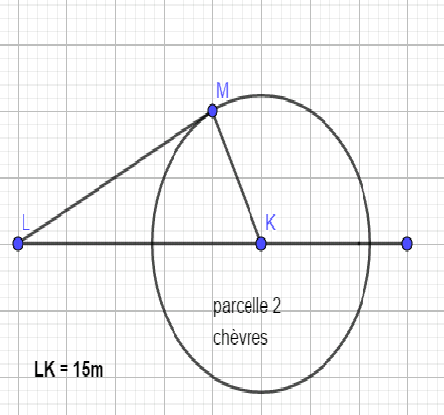
Commented by john santu last updated on 16/Jan/20
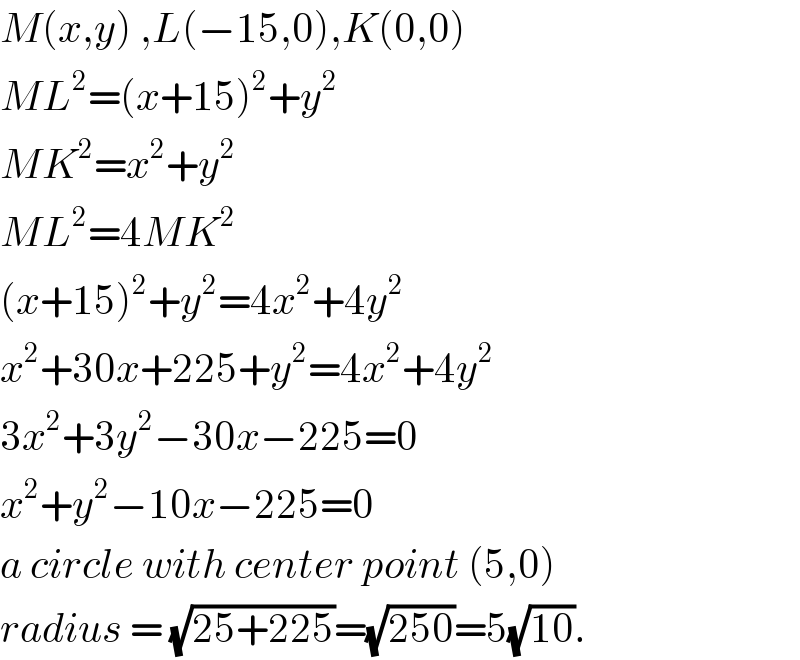
$${M}\left({x},{y}\right)\:,{L}\left(−\mathrm{15},\mathrm{0}\right),{K}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${ML}^{\mathrm{2}} =\left({x}+\mathrm{15}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${MK}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$${ML}^{\mathrm{2}} =\mathrm{4}{MK}^{\mathrm{2}} \\ $$$$\left({x}+\mathrm{15}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +\mathrm{30}{x}+\mathrm{225}+{y}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{y}^{\mathrm{2}} −\mathrm{30}{x}−\mathrm{225}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{225}=\mathrm{0} \\ $$$${a}\:{circle}\:{with}\:{center}\:{point}\:\left(\mathrm{5},\mathrm{0}\right) \\ $$$${radius}\:=\:\sqrt{\mathrm{25}+\mathrm{225}}=\sqrt{\mathrm{250}}=\mathrm{5}\sqrt{\mathrm{10}}. \\ $$
