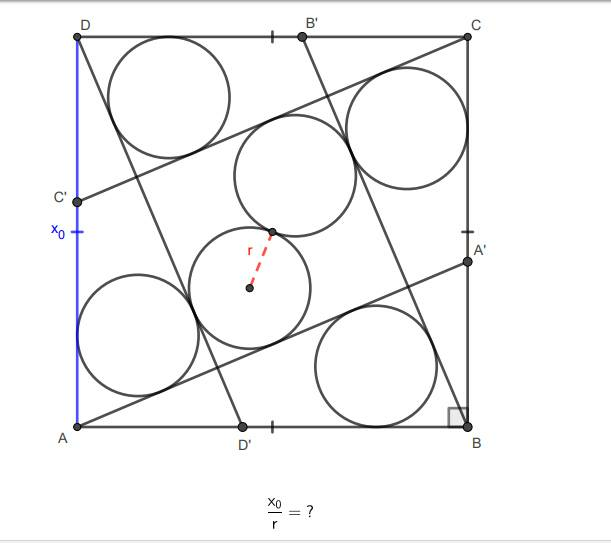
Question Number 78443 by Maclaurin Stickker last updated on 17/Jan/20
Answered by mr W last updated on 18/Jan/20
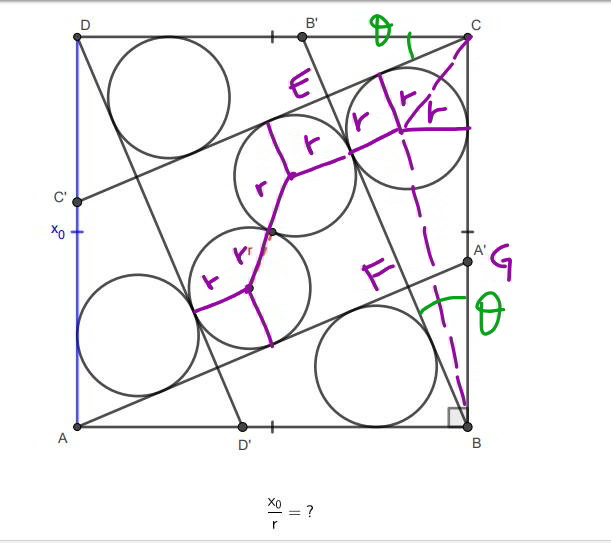
Commented by mr W last updated on 18/Jan/20

$${side}\:{length}\:{of}\:{square}\:={a}={x}_{\mathrm{0}} \\ $$$${EF}=\mathrm{2}{r}+\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{2}}}=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){r} \\ $$$${EB}={r}+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}={a}\:\mathrm{cos}\:\theta\:\Rightarrow\frac{{a}}{{r}}=\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}}{\mathrm{cos}\:\theta} \\ $$$${EC}={r}+\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)}={FB} \\ $$$${EB}={EF}+{FB} \\ $$$${r}+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){r}+{r}+\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}=\mathrm{2}+\sqrt{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{\theta}{\mathrm{2}}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}=\mathrm{2}+\sqrt{\mathrm{2}}+\frac{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$$${let}\:{t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){t}^{\mathrm{2}} −\left(\mathrm{4}+\sqrt{\mathrm{2}}\right){t}+\mathrm{1}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{4}+\sqrt{\mathrm{2}}−\sqrt{\left(\mathrm{4}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}}{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$${t}=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}−\mathrm{2}−\sqrt{\mathrm{2}\left(\mathrm{13}−\mathrm{8}\sqrt{\mathrm{2}}\right)}}{\mathrm{2}}\:\Rightarrow\theta=\mathrm{22}.\mathrm{96}° \\ $$$$\frac{{x}_{\mathrm{0}} }{{r}}=\frac{{a}}{{r}}=\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}}{\mathrm{cos}\:\theta}=\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}\right){t}}=\mathrm{6}.\mathrm{4336} \\ $$
