Menu Close

find-the-point-on-the-graph-of-f-x-1-x-2-that-are-closest-to-O-0-0-

Tinku Tara
Pin




Question Number 131188 by abdurehime last updated on 02/Feb/21
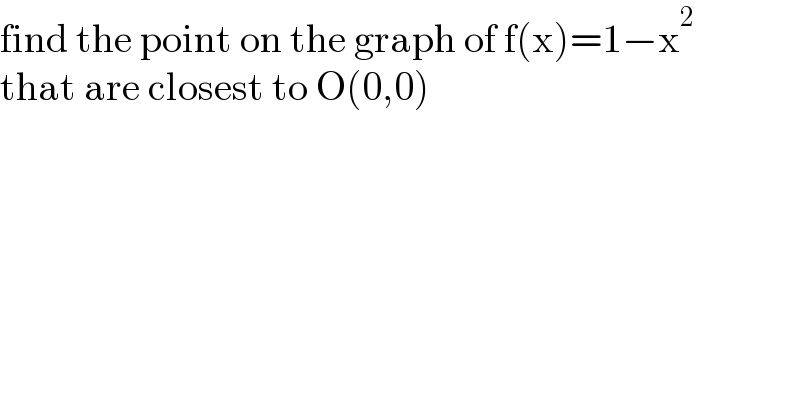
find the point on the graph of f(x)=1−x^2 that are closest to O(0,0)
$$\mathrm{find}\:\mathrm{the}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{graph}\:\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{1}−\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{that}\:\mathrm{are}\:\mathrm{closest}\:\mathrm{to}\:\mathrm{O}\left(\mathrm{0},\mathrm{0}\right) \\ $$
Answered by john_santu last updated on 02/Feb/21
let P(x,y) is the point on the curve. let the distance between point P to point O = d =(√(x^2 +y^2 )) = (√(1−y+y^2 )) or d^2 = y^2 −y+1 ; y^2 −y+1−d^2 = 0 by tangency Δ =0 ⇒ 1−4(1−d^2 ) = 0; 1−d^2 = (1/4) ⇒d^2 =(3/4) ⇒y^2 −y+(1/4)=0 (y−(1/2))^2 = 0 → { ((y=(1/2))),((x=±(1/2)(√2))) :} we get → { ((P_1 ((1/2)(√2) ,(1/2)))),((P_2 (−(1/2)(√2) , (1/2)))) :}
$${let}\:{P}\left({x},{y}\right)\:{is}\:{the}\:{point}\:{on}\:{the} \\ $$$${curve}.\: \\ $$$${let}\:{the}\:{distance}\:{between}\:{point}\:{P}\:{to}\:{point}\:{O} \\ $$$$=\:{d}\:=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:=\:\sqrt{\mathrm{1}−{y}+{y}^{\mathrm{2}} } \\ $$$${or}\:{d}^{\mathrm{2}} \:=\:{y}^{\mathrm{2}} −{y}+\mathrm{1}\:;\:{y}^{\mathrm{2}} −{y}+\mathrm{1}−{d}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$${by}\:{tangency}\:\Delta\:=\mathrm{0}\: \\ $$$$\Rightarrow\:\mathrm{1}−\mathrm{4}\left(\mathrm{1}−{d}^{\mathrm{2}} \right)\:=\:\mathrm{0};\:\mathrm{1}−{d}^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{d}^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}}\:\Rightarrow{y}^{\mathrm{2}} −{y}+\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\:\left({y}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{0}\:\rightarrow\begin{cases}{{y}=\frac{\mathrm{1}}{\mathrm{2}}}\\{{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}}\end{cases} \\ $$$${we}\:{get}\:\rightarrow\begin{cases}{{P}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:,\frac{\mathrm{1}}{\mathrm{2}}\right)}\\{{P}_{\mathrm{2}} \left(−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:,\:\frac{\mathrm{1}}{\mathrm{2}}\right)}\end{cases} \\ $$
Commented by abdurehime last updated on 02/Feb/21
i satisfied 100% allh bless you
$$\mathrm{i}\:\mathrm{satisfied}\:\mathrm{100\%}\:\mathrm{allh}\:\mathrm{bless}\:\mathrm{you} \\ $$
Answered by mr W last updated on 02/Feb/21
say the point is (x,y) with y=1−x^2 the distance from (x,y) to (0,0) is d. d^2 =x^2 +y^2 =x^2 +(1−x^2 )^2 =x^4 −x^2 +1 =(x^2 −(1/2))^2 +(3/4)≥(3/4) ⇒d_(min) =(√(3/4))=((√3)/2) at x^2 =(1/2) ⇒x=±((√2)/2), y=1−(1/2)=(1/2) ⇒point (−((√2)/2),(1/2)) or point (((√2)/2),(1/2))
$${say}\:{the}\:{point}\:{is}\:\left({x},{y}\right)\:{with} \\ $$$${y}=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${the}\:{distance}\:{from}\:\left({x},{y}\right)\:{to}\:\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{d}. \\ $$$${d}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={x}^{\mathrm{2}} +\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$={x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$=\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\geqslant\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{d}_{{min}} =\sqrt{\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${at}\:{x}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{x}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:{y}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{point}\:\left(−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)\:{or}\:{point}\:\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$

Pin