Menu Close

Solve-the-equation-x-2-y-z-2-10-i-y-2-z-x-2-5-ii-z-2-x-y-2-2-iii-

Tinku Tara 0 Comments
Pin




Question Number 78694 by TawaTawa last updated on 19/Jan/20
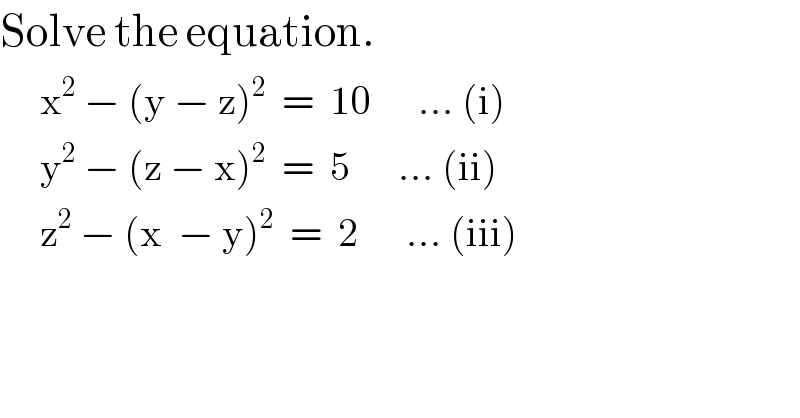
Solve the equation. x^2 − (y − z)^2 = 10 ... (i) y^2 − (z − x)^2 = 5 ... (ii) z^2 − (x − y)^2 = 2 ... (iii)
$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{equation}. \\ $$$$\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:−\:\left(\mathrm{y}\:−\:\mathrm{z}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{10}\:\:\:\:\:\:…\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\mathrm{y}^{\mathrm{2}} \:−\:\left(\mathrm{z}\:−\:\mathrm{x}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{5}\:\:\:\:\:\:…\:\left(\mathrm{ii}\right) \\ $$$$\:\:\:\:\:\mathrm{z}^{\mathrm{2}} \:−\:\left(\mathrm{x}\:\:−\:\mathrm{y}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{2}\:\:\:\:\:\:…\:\left(\mathrm{iii}\right) \\ $$
Commented by john santu last updated on 20/Jan/20
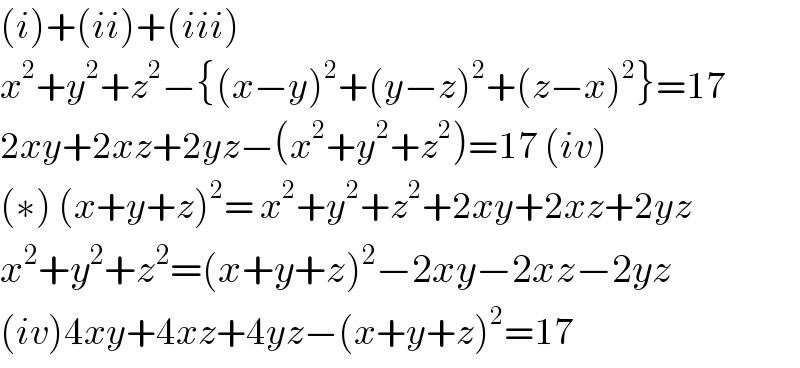
(i)+(ii)+(iii) x^2 +y^2 +z^2 −{(x−y)^2 +(y−z)^2 +(z−x)^2 }=17 2xy+2xz+2yz−(x^2 +y^2 +z^2 )=17 (iv) (∗) (x+y+z)^2 = x^2 +y^2 +z^2 +2xy+2xz+2yz x^2 +y^2 +z^2 =(x+y+z)^2 −2xy−2xz−2yz (iv)4xy+4xz+4yz−(x+y+z)^2 =17
$$\left({i}\right)+\left({ii}\right)+\left({iii}\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} −\left\{\left({x}−{y}\right)^{\mathrm{2}} +\left({y}−{z}\right)^{\mathrm{2}} +\left({z}−{x}\right)^{\mathrm{2}} \right\}=\mathrm{17} \\ $$$$\mathrm{2}{xy}+\mathrm{2}{xz}+\mathrm{2}{yz}−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)=\mathrm{17}\:\left({iv}\right) \\ $$$$\left(\ast\right)\:\left({x}+{y}+{z}\right)^{\mathrm{2}} =\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{2}{xz}+\mathrm{2}{yz} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\left({x}+{y}+{z}\right)^{\mathrm{2}} −\mathrm{2}{xy}−\mathrm{2}{xz}−\mathrm{2}{yz} \\ $$$$\left({iv}\right)\mathrm{4}{xy}+\mathrm{4}{xz}+\mathrm{4}{yz}−\left({x}+{y}+{z}\right)^{\mathrm{2}} =\mathrm{17} \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Jan/20
x^2 − (y − z)^2 = 10 ... (A) y^2 − (z − x)^2 = 5 ... (B) z^2 − (x − y)^2 = 2 ... (C) A/B:(((x−y+z)(x+y−z))/((y−z+x)(y+z−x)))=((10)/5)=2 x−y+z=2(y+z−x) x−y+z=2y+2z−2x) 3x−3y−z=0........∗ A/C:(((x−y+z)(x+y−z))/((z−x+y)(z+x−y)))=((10)/2)=5 ((x+y−z)/(z−x+y))=5 x+y−z=5z−5x+5y 6x−4y−6z=0 3x−2y−3z=0.........∗∗ B/C:(((y−z+x)(y+z−x))/((z−x+y)(z+x−y)))=(5/2) 5(z+x−y)=2(y−z+x) 3x−7y+3z=0......∗∗∗ ∗ , ∗∗ & ∗∗∗ are simultaneous linear equations in 3 variables and can be solved easily: [((3x−3y−z=0)),((3x−2y−3z=0)),((3x−7y+3z=0)) ]
$$\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:−\:\left(\mathrm{y}\:−\:\mathrm{z}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{10}\:\:\:\:\:\:…\:\left(\mathrm{A}\right) \\ $$$$\:\:\:\:\:\mathrm{y}^{\mathrm{2}} \:−\:\left(\mathrm{z}\:−\:\mathrm{x}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{5}\:\:\:\:\:\:…\:\left(\mathrm{B}\right) \\ $$$$\:\:\:\:\:\mathrm{z}^{\mathrm{2}} \:−\:\left(\mathrm{x}\:\:−\:\mathrm{y}\right)^{\mathrm{2}} \:\:=\:\:\mathrm{2}\:\:\:\:\:\:…\:\left(\mathrm{C}\right) \\ $$$$\mathrm{A}/\mathrm{B}:\frac{\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)}{\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)}=\frac{\mathrm{10}}{\mathrm{5}}=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}−\mathrm{y}+\mathrm{z}=\mathrm{2}\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{x}−\mathrm{y}+\mathrm{z}=\mathrm{2y}+\mathrm{2z}−\mathrm{2x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}−\mathrm{3y}−\mathrm{z}=\mathrm{0}……..\ast \\ $$$$\mathrm{A}/\mathrm{C}:\frac{\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)}{\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)}=\frac{\mathrm{10}}{\mathrm{2}}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{x}+\mathrm{y}−\mathrm{z}}{\mathrm{z}−\mathrm{x}+\mathrm{y}}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{x}+\mathrm{y}−\mathrm{z}=\mathrm{5z}−\mathrm{5x}+\mathrm{5y} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{6x}−\mathrm{4y}−\mathrm{6z}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{3x}−\mathrm{2y}−\mathrm{3z}=\mathrm{0}………\ast\ast \\ $$$$\mathrm{B}/\mathrm{C}:\frac{\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)}{\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)=\mathrm{2}\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3x}−\mathrm{7y}+\mathrm{3z}=\mathrm{0}……\ast\ast\ast \\ $$$$ \\ $$$$\ast\:,\:\ast\ast\:\&\:\ast\ast\ast\:\mathrm{are}\:\mathrm{simultaneous}\:\mathrm{linear}\:\mathrm{equations} \\ $$$$\mathrm{in}\:\mathrm{3}\:\mathrm{variables}\:\mathrm{and}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\: \\ $$$$\mathrm{easily}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\begin{bmatrix}{\mathrm{3x}−\mathrm{3y}−\mathrm{z}=\mathrm{0}}\\{\mathrm{3x}−\mathrm{2y}−\mathrm{3z}=\mathrm{0}}\\{\mathrm{3x}−\mathrm{7y}+\mathrm{3z}=\mathrm{0}}\end{bmatrix} \\ $$$$\:\:\:\:\:\:\:\: \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by jagoll last updated on 20/Jan/20
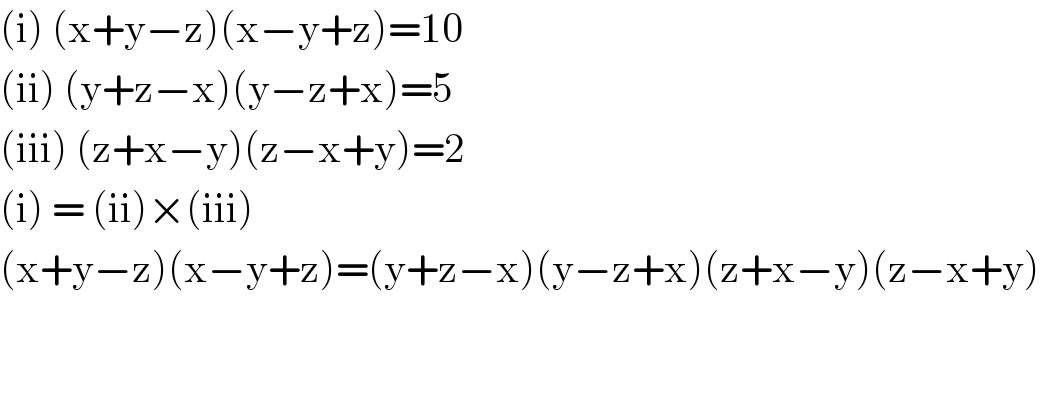
(i) (x+y−z)(x−y+z)=10 (ii) (y+z−x)(y−z+x)=5 (iii) (z+x−y)(z−x+y)=2 (i) = (ii)×(iii) (x+y−z)(x−y+z)=(y+z−x)(y−z+x)(z+x−y)(z−x+y)
$$\left(\mathrm{i}\right)\:\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)=\mathrm{10} \\ $$$$\left(\mathrm{ii}\right)\:\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)=\mathrm{5} \\ $$$$\left(\mathrm{iii}\right)\:\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)=\mathrm{2} \\ $$$$\left(\mathrm{i}\right)\:=\:\left(\mathrm{ii}\right)×\left(\mathrm{iii}\right) \\ $$$$\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)=\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by jagoll last updated on 20/Jan/20
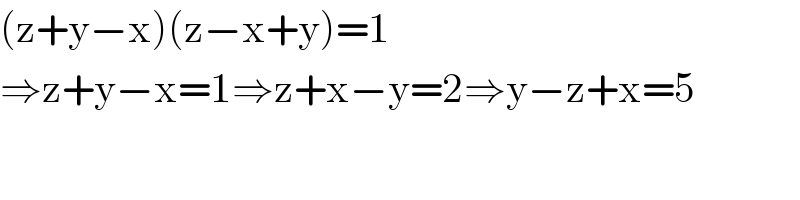
(z+y−x)(z−x+y)=1 ⇒z+y−x=1⇒z+x−y=2⇒y−z+x=5
$$\left(\mathrm{z}+\mathrm{y}−\mathrm{x}\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{z}+\mathrm{y}−\mathrm{x}=\mathrm{1}\Rightarrow\mathrm{z}+\mathrm{x}−\mathrm{y}=\mathrm{2}\Rightarrow\mathrm{y}−\mathrm{z}+\mathrm{x}=\mathrm{5} \\ $$$$ \\ $$
Commented by mr W last updated on 20/Jan/20
your approch is not “exact” mathematically, i think. what if the equations were e.g.: (i) (x+y−z)(x−y+z)=7 (ii) (y+z−x)(y−z+x)=11 (iii) (z+x−y)(z−x+y)=2 ? then you can not simply guess the values for x+y−z etc. and reach the correct solution by accident.
$${your}\:{approch}\:{is}\:{not}\:“{exact}''\:{mathematically}, \\ $$$${i}\:{think}. \\ $$$${what}\:{if}\:{the}\:{equations}\:{were}\:{e}.{g}.: \\ $$$$\left(\mathrm{i}\right)\:\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)=\mathrm{7} \\ $$$$\left(\mathrm{ii}\right)\:\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)=\mathrm{11} \\ $$$$\left(\mathrm{iii}\right)\:\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)=\mathrm{2}\:? \\ $$$${then}\:{you}\:{can}\:{not}\:{simply}\:{guess}\:{the}\:{values} \\ $$$${for}\:\mathrm{x}+\mathrm{y}−\mathrm{z}\:{etc}.\:{and}\:{reach}\:{the}\:{correct} \\ $$$${solution}\:{by}\:{accident}. \\ $$
Commented by jagoll last updated on 20/Jan/20
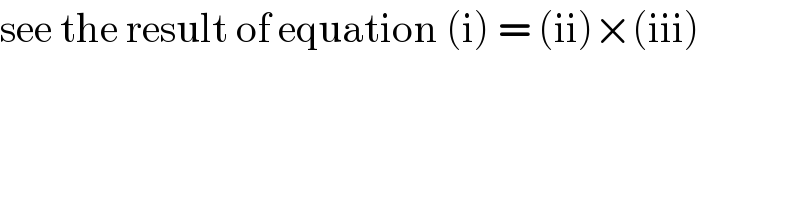
see the result of equation (i) = (ii)×(iii)
$$\mathrm{see}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{equation}\:\left(\mathrm{i}\right)\:=\:\left(\mathrm{ii}\right)×\left(\mathrm{iii}\right) \\ $$
Commented by jagoll last updated on 20/Jan/20
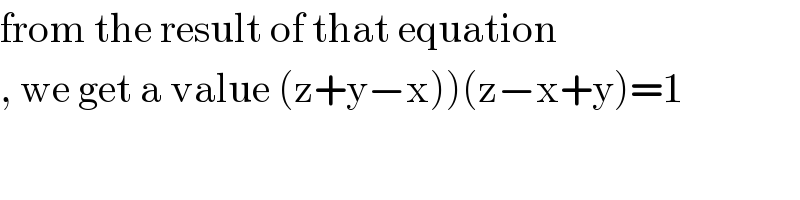
from the result of that equation , we get a value (z+y−x))(z−x+y)=1
$$\mathrm{from}\:\mathrm{the}\:\mathrm{result}\:\mathrm{of}\:\mathrm{that}\:\mathrm{equation} \\ $$$$\left.,\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{value}\:\left(\mathrm{z}+\mathrm{y}−\mathrm{x}\right)\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)=\mathrm{1} \\ $$
Commented by jagoll last updated on 20/Jan/20
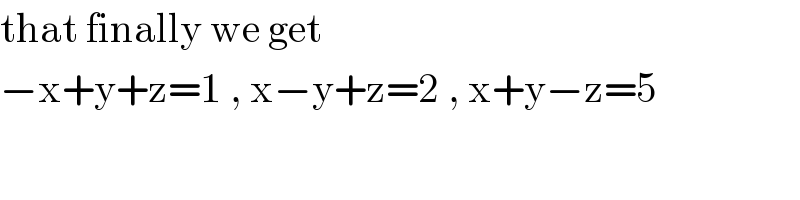
that finally we get −x+y+z=1 , x−y+z=2 , x+y−z=5
$$\mathrm{that}\:\mathrm{finally}\:\mathrm{we}\:\mathrm{get}\: \\ $$$$−\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1}\:,\:\mathrm{x}−\mathrm{y}+\mathrm{z}=\mathrm{2}\:,\:\mathrm{x}+\mathrm{y}−\mathrm{z}=\mathrm{5} \\ $$
Commented by jagoll last updated on 20/Jan/20
don′t play that guess sir. there is process, which i shorten the process
$$\mathrm{don}'\mathrm{t}\:\mathrm{play}\:\mathrm{that}\:\mathrm{guess}\:\mathrm{sir}.\:\mathrm{there} \\ $$$$\mathrm{is}\:\mathrm{process},\:\mathrm{which}\:\mathrm{i}\:\mathrm{shorten}\:\mathrm{the} \\ $$$$\mathrm{process} \\ $$
Commented by mr W last updated on 20/Jan/20
maybe i didn′t unterstand your method correctly. i thought you just guess the following values: ⇒z+y−x=1⇒z+x−y=2⇒y−z+x=5 ? or can you share how you get them? besides, the original equations are 3 quadratical relations between x,y,z. but you could reduce them to 3 linear relations. how did you get this? and can you find the solution using your method if the equations are: (i) (x+y−z)(x−y+z)=7 (ii) (y+z−x)(y−z+x)=11 (iii) (z+x−y)(z−x+y)=2 if there is an easier method, i want to learn.
$${maybe}\:{i}\:{didn}'{t}\:{unterstand}\:{your}\:{method} \\ $$$${correctly}.\:{i}\:{thought}\:{you}\:{just}\:{guess}\:{the} \\ $$$${following}\:{values}: \\ $$$$\Rightarrow\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{x}}=\mathrm{1}\Rightarrow\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}=\mathrm{2}\Rightarrow\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{z}}+\boldsymbol{\mathrm{x}}=\mathrm{5}\:? \\ $$$${or}\:{can}\:{you}\:{share}\:{how}\:{you}\:{get}\:{them}? \\ $$$$ \\ $$$${besides},\:{the}\:{original}\:{equations}\:{are}\:\mathrm{3} \\ $$$${quadratical}\:{relations}\:{between}\:{x},{y},{z}. \\ $$$${but}\:{you}\:{could}\:{reduce}\:{them}\:{to}\:\mathrm{3}\:{linear}\: \\ $$$${relations}.\:{how}\:{did}\:{you}\:{get}\:{this}? \\ $$$$ \\ $$$${and}\:{can}\:{you}\:{find}\:{the}\:{solution}\:{using} \\ $$$${your}\:{method}\:{if}\:{the}\:{equations}\:{are}: \\ $$$$\left(\mathrm{i}\right)\:\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)=\mathrm{7} \\ $$$$\left(\mathrm{ii}\right)\:\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)\left(\mathrm{y}−\mathrm{z}+\mathrm{x}\right)=\mathrm{11} \\ $$$$\left(\mathrm{iii}\right)\:\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)\left(\mathrm{z}−\mathrm{x}+\mathrm{y}\right)=\mathrm{2} \\ $$$$ \\ $$$${if}\:{there}\:{is}\:{an}\:{easier}\:{method},\:{i}\:{want}\:{to} \\ $$$${learn}.\: \\ $$
Commented by jagoll last updated on 20/Jan/20
ha ha . don′t setence like that sir. i am not a psychic who can guess the answers
$$\mathrm{ha}\:\mathrm{ha}\:.\:\mathrm{don}'\mathrm{t}\:\mathrm{setence}\:\mathrm{like}\:\mathrm{that} \\ $$$$\mathrm{sir}.\:\mathrm{i}\:\mathrm{am}\:\mathrm{not}\:\mathrm{a}\:\mathrm{psychic}\:\mathrm{who}\:\mathrm{can} \\ $$$$\mathrm{guess}\:\mathrm{the}\:\mathrm{answers} \\ $$
Commented by jagoll last updated on 20/Jan/20
Commented by mr W last updated on 20/Jan/20
since you got the correct solution much more directly and faster, i was very interested and wanted to learn how and sincerely asked you for more details. but if you don′t want to tell more about your secret, i respect it sir. thank you!
$${since}\:{you}\:{got}\:{the}\:{correct}\:{solution} \\ $$$${much}\:{more}\:{directly}\:{and}\:{faster},\:{i} \\ $$$${was}\:{very}\:{interested}\:{and}\:{wanted}\:{to} \\ $$$${learn}\:{how}\:{and}\:{sincerely}\:{asked}\:{you} \\ $$$${for}\:{more}\:{details}. \\ $$$${but}\:{if}\:{you}\:{don}'{t}\:{want}\:{to}\:{tell}\:{more}\:{about} \\ $$$${your}\:{secret},\:{i}\:{respect}\:{it}\:{sir}.\:{thank}\:{you}! \\ $$
Commented by jagoll last updated on 20/Jan/20
look sir
$$\mathrm{look}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 20/Jan/20
thanks alot sir!
$${thanks}\:{alot}\:{sir}! \\ $$
Commented by jagoll last updated on 20/Jan/20
yes sir. i didn′t mean to not want to explain it, but i think that asking questions needs a quick response so i cut some of the solutions. thank you sir, for this discussion. i like
$$\mathrm{yes}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{didn}'\mathrm{t}\:\mathrm{mean}\:\mathrm{to}\:\mathrm{not} \\ $$$$\mathrm{want}\:\mathrm{to}\:\mathrm{explain}\:\mathrm{it},\:\mathrm{but}\:\mathrm{i}\:\mathrm{think} \\ $$$$\mathrm{that}\:\mathrm{asking}\:\mathrm{questions}\:\mathrm{needs} \\ $$$$\mathrm{a}\:\mathrm{quick}\:\mathrm{response}\:\mathrm{so}\:\mathrm{i}\:\mathrm{cut}\:\mathrm{some}\:\mathrm{of}\: \\ $$$$\mathrm{the}\:\mathrm{solutions}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{for} \\ $$$$\mathrm{this}\:\mathrm{discussion}.\:\mathrm{i}\:\mathrm{like} \\ $$
Commented by mr W last updated on 20/Jan/20
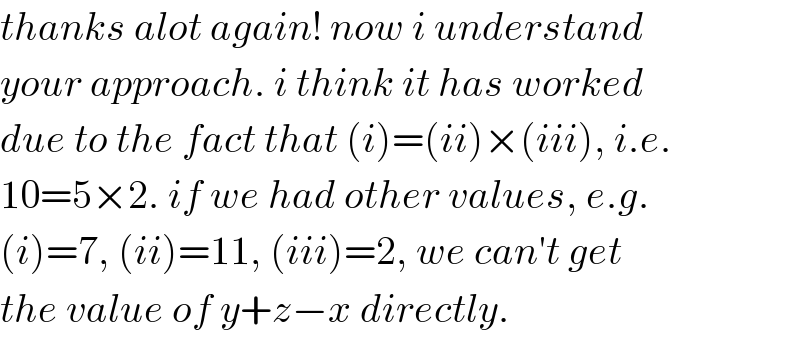
thanks alot again! now i understand your approach. i think it has worked due to the fact that (i)=(ii)×(iii), i.e. 10=5×2. if we had other values, e.g. (i)=7, (ii)=11, (iii)=2, we can′t get the value of y+z−x directly.
$${thanks}\:{alot}\:{again}!\:{now}\:{i}\:{understand} \\ $$$${your}\:{approach}.\:{i}\:{think}\:{it}\:{has}\:{worked} \\ $$$${due}\:{to}\:{the}\:{fact}\:{that}\:\left({i}\right)=\left({ii}\right)×\left({iii}\right),\:{i}.{e}. \\ $$$$\mathrm{10}=\mathrm{5}×\mathrm{2}.\:{if}\:{we}\:{had}\:{other}\:{values},\:{e}.{g}. \\ $$$$\left({i}\right)=\mathrm{7},\:\left({ii}\right)=\mathrm{11},\:\left({iii}\right)=\mathrm{2},\:{we}\:{can}'{t}\:{get} \\ $$$${the}\:{value}\:{of}\:{y}+{z}−{x}\:{directly}. \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by john santu last updated on 21/Jan/20
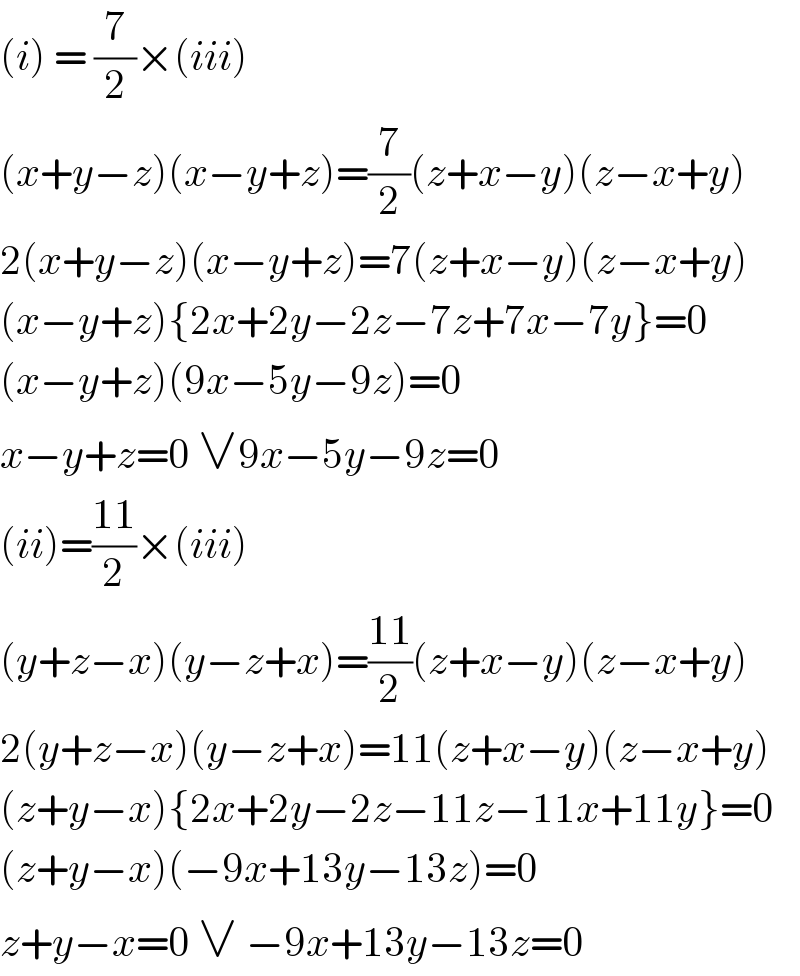
(i) = (7/2)×(iii) (x+y−z)(x−y+z)=(7/2)(z+x−y)(z−x+y) 2(x+y−z)(x−y+z)=7(z+x−y)(z−x+y) (x−y+z){2x+2y−2z−7z+7x−7y}=0 (x−y+z)(9x−5y−9z)=0 x−y+z=0 ∨9x−5y−9z=0 (ii)=((11)/2)×(iii) (y+z−x)(y−z+x)=((11)/2)(z+x−y)(z−x+y) 2(y+z−x)(y−z+x)=11(z+x−y)(z−x+y) (z+y−x){2x+2y−2z−11z−11x+11y}=0 (z+y−x)(−9x+13y−13z)=0 z+y−x=0 ∨ −9x+13y−13z=0
$$\left({i}\right)\:=\:\frac{\mathrm{7}}{\mathrm{2}}×\left({iii}\right) \\ $$$$\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)=\frac{\mathrm{7}}{\mathrm{2}}\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right) \\ $$$$\mathrm{2}\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)=\mathrm{7}\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right) \\ $$$$\left({x}−{y}+{z}\right)\left\{\mathrm{2}{x}+\mathrm{2}{y}−\mathrm{2}{z}−\mathrm{7}{z}+\mathrm{7}{x}−\mathrm{7}{y}\right\}=\mathrm{0} \\ $$$$\left({x}−{y}+{z}\right)\left(\mathrm{9}{x}−\mathrm{5}{y}−\mathrm{9}{z}\right)=\mathrm{0} \\ $$$${x}−{y}+{z}=\mathrm{0}\:\vee\mathrm{9}{x}−\mathrm{5}{y}−\mathrm{9}{z}=\mathrm{0} \\ $$$$\left({ii}\right)=\frac{\mathrm{11}}{\mathrm{2}}×\left({iii}\right) \\ $$$$\left({y}+{z}−{x}\right)\left({y}−{z}+{x}\right)=\frac{\mathrm{11}}{\mathrm{2}}\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right) \\ $$$$\mathrm{2}\left({y}+{z}−{x}\right)\left({y}−{z}+{x}\right)=\mathrm{11}\left({z}+{x}−{y}\right)\left({z}−{x}+{y}\right) \\ $$$$\left({z}+{y}−{x}\right)\left\{\mathrm{2}{x}+\mathrm{2}{y}−\mathrm{2}{z}−\mathrm{11}{z}−\mathrm{11}{x}+\mathrm{11}{y}\right\}=\mathrm{0} \\ $$$$\left({z}+{y}−{x}\right)\left(−\mathrm{9}{x}+\mathrm{13}{y}−\mathrm{13}{z}\right)=\mathrm{0} \\ $$$${z}+{y}−{x}=\mathrm{0}\:\vee\:−\mathrm{9}{x}+\mathrm{13}{y}−\mathrm{13}{z}=\mathrm{0} \\ $$
Commented by john santu last updated on 21/Jan/20
to Mr W. i am interested in the questions in you made and solve them with the concept of MrJagoll. i think the concept of Mr Jagoll is not a mathematical concept but a tactical thinking concept. i appreciate Mr Jagoll, because no one in the world can argue 10 = 5×2. i′m not on anyone′s side, but i try to express my thoughts that mathematics must be able to make someone creative in solving problems. thanks you
$${to}\:{Mr}\:{W}. \\ $$$${i}\:{am}\:{interested}\:{in}\:{the}\:{questions}\: \\ $$$${in}\:{you}\:{made}\:{and}\:{solve}\:{them}\: \\ $$$${with}\:{the}\:{concept}\:{of}\:{MrJagoll}. \\ $$$${i}\:{think}\:{the}\:{concept}\:{of}\:{Mr}\:{Jagoll} \\ $$$${is}\:{not}\:{a}\:{mathematical}\:{concept} \\ $$$${but}\:{a}\:{tactical}\:{thinking}\:{concept}. \\ $$$${i}\:{appreciate}\:{Mr}\:{Jagoll},\:{because} \\ $$$${no}\:{one}\:{in}\:{the}\:{world}\:{can}\:{argue} \\ $$$$\mathrm{10}\:=\:\mathrm{5}×\mathrm{2}.\:{i}'{m}\:{not}\:{on}\:{anyone}'{s} \\ $$$${side},\:{but}\:{i}\:{try}\:{to}\:{express}\:{my} \\ $$$${thoughts}\:{that}\:{mathematics} \\ $$$${must}\:{be}\:{able}\:{to}\:{make}\:{someone} \\ $$$${creative}\:{in}\:{solving}\:{problems}. \\ $$$${thanks}\:{you} \\ $$$$ \\ $$
Commented by mr W last updated on 21/Jan/20
yes sir! being creative is also that what i appreciate and what i try to be.
$${yes}\:{sir}!\:{being}\:{creative}\:{is}\:{also}\:{that} \\ $$$${what}\:{i}\:{appreciate}\:{and}\:{what}\:{i}\:{try}\:{to}\:{be}.\: \\ $$
Answered by jagoll last updated on 20/Jan/20
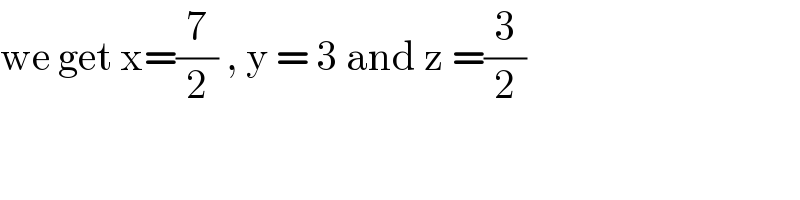
we get x=(7/2) , y = 3 and z =(3/2)
$$\mathrm{we}\:\mathrm{get}\:\mathrm{x}=\frac{\mathrm{7}}{\mathrm{2}}\:,\:\mathrm{y}\:=\:\mathrm{3}\:\mathrm{and}\:\mathrm{z}\:=\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 20/Jan/20
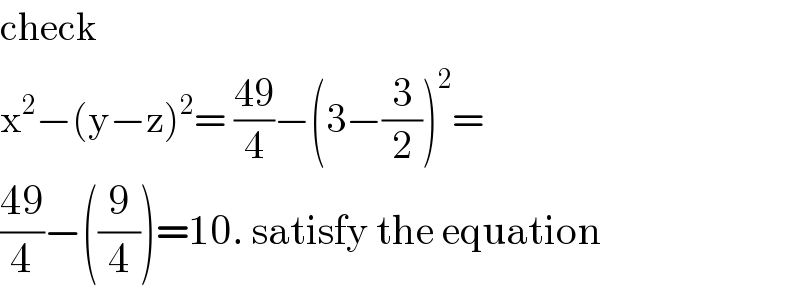
check x^2 −(y−z)^2 = ((49)/4)−(3−(3/2))^2 = ((49)/4)−((9/4))=10. satisfy the equation
$$\mathrm{check}\: \\ $$$$\mathrm{x}^{\mathrm{2}} −\left(\mathrm{y}−\mathrm{z}\right)^{\mathrm{2}} =\:\frac{\mathrm{49}}{\mathrm{4}}−\left(\mathrm{3}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} = \\ $$$$\frac{\mathrm{49}}{\mathrm{4}}−\left(\frac{\mathrm{9}}{\mathrm{4}}\right)=\mathrm{10}.\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation} \\ $$
Answered by mr W last updated on 20/Jan/20
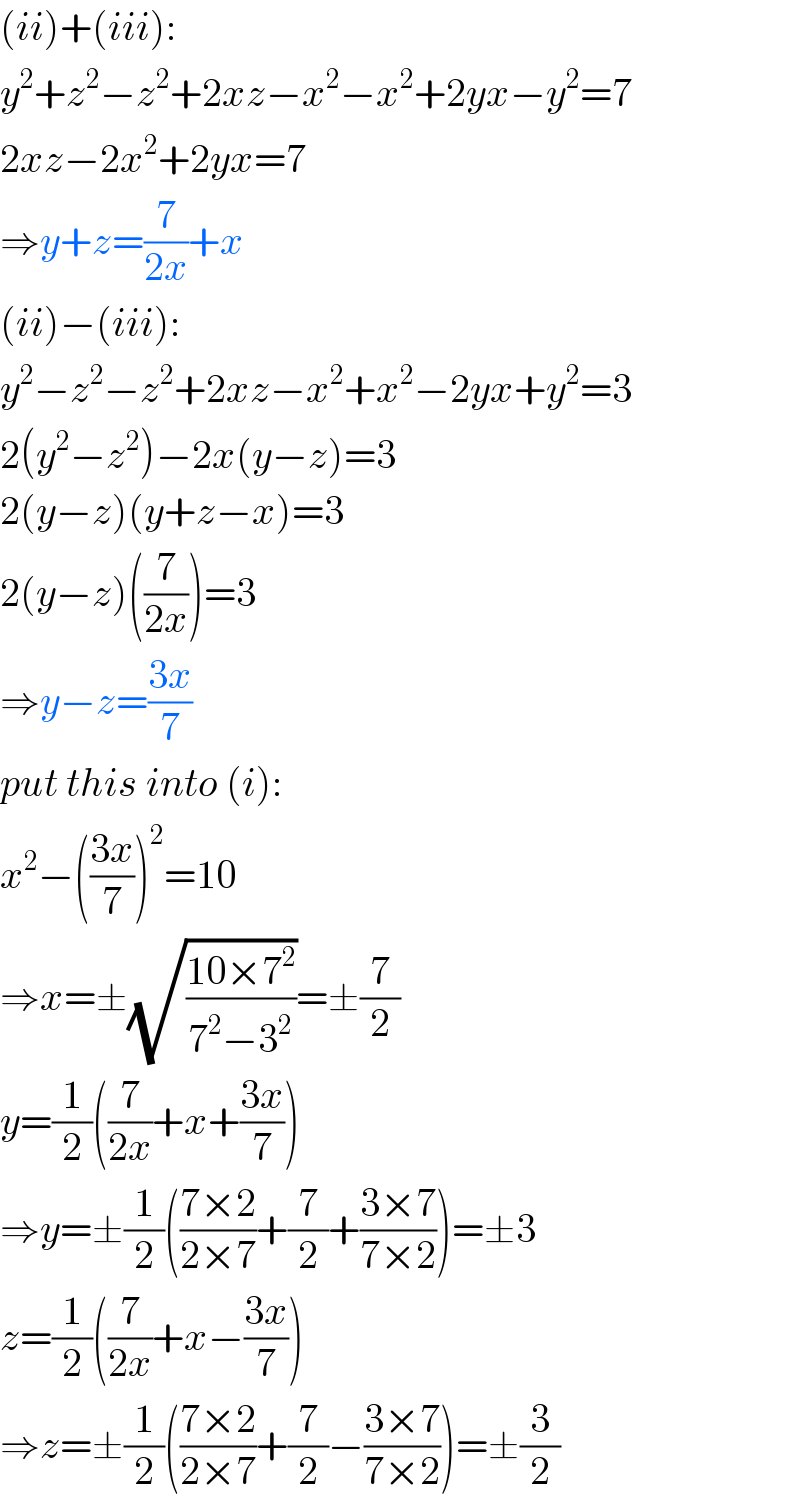
(ii)+(iii): y^2 +z^2 −z^2 +2xz−x^2 −x^2 +2yx−y^2 =7 2xz−2x^2 +2yx=7 ⇒y+z=(7/(2x))+x (ii)−(iii): y^2 −z^2 −z^2 +2xz−x^2 +x^2 −2yx+y^2 =3 2(y^2 −z^2 )−2x(y−z)=3 2(y−z)(y+z−x)=3 2(y−z)((7/(2x)))=3 ⇒y−z=((3x)/7) put this into (i): x^2 −(((3x)/7))^2 =10 ⇒x=±(√((10×7^2 )/(7^2 −3^2 )))=±(7/2) y=(1/2)((7/(2x))+x+((3x)/7)) ⇒y=±(1/2)(((7×2)/(2×7))+(7/2)+((3×7)/(7×2)))=±3 z=(1/2)((7/(2x))+x−((3x)/7)) ⇒z=±(1/2)(((7×2)/(2×7))+(7/2)−((3×7)/(7×2)))=±(3/2)
$$\left({ii}\right)+\left({iii}\right): \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} −{z}^{\mathrm{2}} +\mathrm{2}{xz}−{x}^{\mathrm{2}} −{x}^{\mathrm{2}} +\mathrm{2}{yx}−{y}^{\mathrm{2}} =\mathrm{7} \\ $$$$\mathrm{2}{xz}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{yx}=\mathrm{7} \\ $$$$\Rightarrow{y}+{z}=\frac{\mathrm{7}}{\mathrm{2}{x}}+{x} \\ $$$$\left({ii}\right)−\left({iii}\right): \\ $$$${y}^{\mathrm{2}} −{z}^{\mathrm{2}} −{z}^{\mathrm{2}} +\mathrm{2}{xz}−{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{yx}+{y}^{\mathrm{2}} =\mathrm{3} \\ $$$$\mathrm{2}\left({y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)−\mathrm{2}{x}\left({y}−{z}\right)=\mathrm{3} \\ $$$$\mathrm{2}\left({y}−{z}\right)\left({y}+{z}−{x}\right)=\mathrm{3} \\ $$$$\mathrm{2}\left({y}−{z}\right)\left(\frac{\mathrm{7}}{\mathrm{2}{x}}\right)=\mathrm{3} \\ $$$$\Rightarrow{y}−{z}=\frac{\mathrm{3}{x}}{\mathrm{7}} \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$${x}^{\mathrm{2}} −\left(\frac{\mathrm{3}{x}}{\mathrm{7}}\right)^{\mathrm{2}} =\mathrm{10} \\ $$$$\Rightarrow{x}=\pm\sqrt{\frac{\mathrm{10}×\mathrm{7}^{\mathrm{2}} }{\mathrm{7}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }}=\pm\frac{\mathrm{7}}{\mathrm{2}} \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}}{\mathrm{2}{x}}+{x}+\frac{\mathrm{3}{x}}{\mathrm{7}}\right) \\ $$$$\Rightarrow{y}=\pm\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}×\mathrm{2}}{\mathrm{2}×\mathrm{7}}+\frac{\mathrm{7}}{\mathrm{2}}+\frac{\mathrm{3}×\mathrm{7}}{\mathrm{7}×\mathrm{2}}\right)=\pm\mathrm{3} \\ $$$${z}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}}{\mathrm{2}{x}}+{x}−\frac{\mathrm{3}{x}}{\mathrm{7}}\right) \\ $$$$\Rightarrow{z}=\pm\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}×\mathrm{2}}{\mathrm{2}×\mathrm{7}}+\frac{\mathrm{7}}{\mathrm{2}}−\frac{\mathrm{3}×\mathrm{7}}{\mathrm{7}×\mathrm{2}}\right)=\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by jagoll last updated on 20/Jan/20
i only took 1 side of the solution. good sir
$$\mathrm{i}\:\mathrm{only}\:\mathrm{took}\:\mathrm{1}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{good} \\ $$$$\mathrm{sir} \\ $$
Commented by jagoll last updated on 20/Jan/20
this settlement is good sir. i have the view according to my father′s military upbringing in solving problems to be fast and on target.
$$\mathrm{this}\:\mathrm{settlement}\:\mathrm{is}\:\mathrm{good}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{have} \\ $$$$\mathrm{the}\:\mathrm{view}\:\mathrm{according}\:\mathrm{to}\:\mathrm{my} \\ $$$$\mathrm{father}'\mathrm{s}\:\mathrm{military}\:\mathrm{upbringing} \\ $$$$\mathrm{in}\:\mathrm{solving}\:\mathrm{problems}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{fast}\:\mathrm{and}\:\mathrm{on}\:\mathrm{target}. \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 20/Jan/20
my solution is valid generally for any values of the equations: (i): .....=a (ii): .....=b (iii): .....=c ⇒x=±(√((a(b+c)^2 )/(4bc))) ⇒y=(1/2)(((b+c)/(2x))+((2bx)/(b+c))) ⇒z=(1/2)(((b+c)/(2x))+((2cx)/(b+c)))
$${my}\:{solution}\:{is}\:{valid}\:{generally}\:{for}\:{any} \\ $$$${values}\:{of}\:{the}\:{equations}: \\ $$$$\left({i}\right):\:\:\:\:\:\:\:…..={a} \\ $$$$\left({ii}\right):\:\:\:\:\:\:\:…..={b} \\ $$$$\left({iii}\right):\:\:\:\:\:\:\:…..={c} \\ $$$$\Rightarrow{x}=\pm\sqrt{\frac{{a}\left({b}+{c}\right)^{\mathrm{2}} }{\mathrm{4}{bc}}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{b}+{c}}{\mathrm{2}{x}}+\frac{\mathrm{2}{bx}}{{b}+{c}}\right) \\ $$$$\Rightarrow{z}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{b}+{c}}{\mathrm{2}{x}}+\frac{\mathrm{2}{cx}}{{b}+{c}}\right) \\ $$
Commented by TawaTawa last updated on 20/Jan/20
Wow, God bless you sir
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 20/Jan/20
absolutely sir!
$${absolutely}\:{sir}! \\ $$
Answered by MJS last updated on 20/Jan/20
let x=u−v∧y=u+v (1) −(2u−z)(2v−z)=10 (2) (2u−z)(2v+z)=5 (3) −(2v+z)(2v−z)=2 (1) v=((2uz−z^2 −10)/(2(2u−z))) (2) 2(2uz−z^2 −5)=5 ⇒ u=((2z^2 +15)/(4z)) ⇒ v=−(z/6) (3) (8/9)z^2 =2 ⇒ z=±(3/2) ⇒ u=±((13)/4)∧v=∓(1/4) ⇒ x=±(7/2)∧y=±3
$$\mathrm{let}\:{x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\left(\mathrm{1}\right)\:\:−\left(\mathrm{2}{u}−{z}\right)\left(\mathrm{2}{v}−{z}\right)=\mathrm{10} \\ $$$$\left(\mathrm{2}\right)\:\:\left(\mathrm{2}{u}−{z}\right)\left(\mathrm{2}{v}+{z}\right)=\mathrm{5} \\ $$$$\left(\mathrm{3}\right)\:\:−\left(\mathrm{2}{v}+{z}\right)\left(\mathrm{2}{v}−{z}\right)=\mathrm{2} \\ $$$$\left(\mathrm{1}\right)\:\:{v}=\frac{\mathrm{2}{uz}−{z}^{\mathrm{2}} −\mathrm{10}}{\mathrm{2}\left(\mathrm{2}{u}−{z}\right)} \\ $$$$\left(\mathrm{2}\right)\:\:\mathrm{2}\left(\mathrm{2}{uz}−{z}^{\mathrm{2}} −\mathrm{5}\right)=\mathrm{5}\:\Rightarrow\:{u}=\frac{\mathrm{2}{z}^{\mathrm{2}} +\mathrm{15}}{\mathrm{4}{z}} \\ $$$$\Rightarrow\:{v}=−\frac{{z}}{\mathrm{6}} \\ $$$$\left(\mathrm{3}\right)\:\:\frac{\mathrm{8}}{\mathrm{9}}{z}^{\mathrm{2}} =\mathrm{2}\:\Rightarrow\:{z}=\pm\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\:{u}=\pm\frac{\mathrm{13}}{\mathrm{4}}\wedge{v}=\mp\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}=\pm\frac{\mathrm{7}}{\mathrm{2}}\wedge{y}=\pm\mathrm{3} \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by behi83417@gmail.com last updated on 20/Jan/20
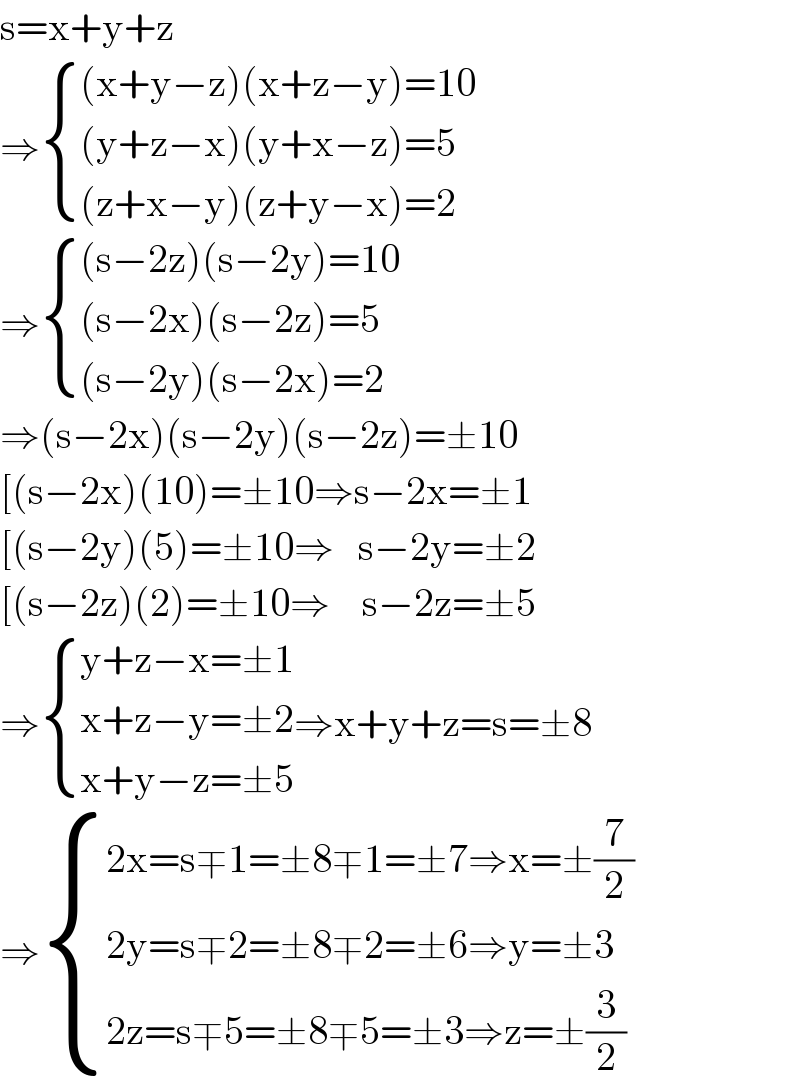
s=x+y+z ⇒ { (((x+y−z)(x+z−y)=10)),(((y+z−x)(y+x−z)=5)),(((z+x−y)(z+y−x)=2)) :} ⇒ { (((s−2z)(s−2y)=10)),(((s−2x)(s−2z)=5)),(((s−2y)(s−2x)=2)) :} ⇒(s−2x)(s−2y)(s−2z)=±10 [(s−2x)(10)=±10⇒s−2x=±1 [(s−2y)(5)=±10⇒ s−2y=±2 [(s−2z)(2)=±10⇒ s−2z=±5 ⇒ { ((y+z−x=±1)),((x+z−y=±2)),((x+y−z=±5)) :}⇒x+y+z=s=±8 ⇒ { ((2x=s∓1=±8∓1=±7⇒x=±(7/2))),((2y=s∓2=±8∓2=±6⇒y=±3)),((2z=s∓5=±8∓5=±3⇒z=±(3/2))) :}
$$\mathrm{s}=\mathrm{x}+\mathrm{y}+\mathrm{z} \\ $$$$\Rightarrow\begin{cases}{\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}+\mathrm{z}−\mathrm{y}\right)=\mathrm{10}}\\{\left(\mathrm{y}+\mathrm{z}−\mathrm{x}\right)\left(\mathrm{y}+\mathrm{x}−\mathrm{z}\right)=\mathrm{5}}\\{\left(\mathrm{z}+\mathrm{x}−\mathrm{y}\right)\left(\mathrm{z}+\mathrm{y}−\mathrm{x}\right)=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\left(\mathrm{s}−\mathrm{2z}\right)\left(\mathrm{s}−\mathrm{2y}\right)=\mathrm{10}}\\{\left(\mathrm{s}−\mathrm{2x}\right)\left(\mathrm{s}−\mathrm{2z}\right)=\mathrm{5}}\\{\left(\mathrm{s}−\mathrm{2y}\right)\left(\mathrm{s}−\mathrm{2x}\right)=\mathrm{2}}\end{cases} \\ $$$$\Rightarrow\left(\mathrm{s}−\mathrm{2x}\right)\left(\mathrm{s}−\mathrm{2y}\right)\left(\mathrm{s}−\mathrm{2z}\right)=\pm\mathrm{10} \\ $$$$\left[\left(\mathrm{s}−\mathrm{2x}\right)\left(\mathrm{10}\right)=\pm\mathrm{10}\Rightarrow\mathrm{s}−\mathrm{2x}=\pm\mathrm{1}\right. \\ $$$$\left[\left(\mathrm{s}−\mathrm{2y}\right)\left(\mathrm{5}\right)=\pm\mathrm{10}\Rightarrow\:\:\:\mathrm{s}−\mathrm{2y}=\pm\mathrm{2}\right. \\ $$$$\left[\left(\mathrm{s}−\mathrm{2z}\right)\left(\mathrm{2}\right)=\pm\mathrm{10}\Rightarrow\:\:\:\:\mathrm{s}−\mathrm{2z}=\pm\mathrm{5}\right. \\ $$$$\Rightarrow\begin{cases}{\mathrm{y}+\mathrm{z}−\mathrm{x}=\pm\mathrm{1}}\\{\mathrm{x}+\mathrm{z}−\mathrm{y}=\pm\mathrm{2}}\\{\mathrm{x}+\mathrm{y}−\mathrm{z}=\pm\mathrm{5}}\end{cases}\Rightarrow\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{s}=\pm\mathrm{8} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2x}=\mathrm{s}\mp\mathrm{1}=\pm\mathrm{8}\mp\mathrm{1}=\pm\mathrm{7}\Rightarrow\mathrm{x}=\pm\frac{\mathrm{7}}{\mathrm{2}}}\\{\mathrm{2y}=\mathrm{s}\mp\mathrm{2}=\pm\mathrm{8}\mp\mathrm{2}=\pm\mathrm{6}\Rightarrow\mathrm{y}=\pm\mathrm{3}}\\{\mathrm{2z}=\mathrm{s}\mp\mathrm{5}=\pm\mathrm{8}\mp\mathrm{5}=\pm\mathrm{3}\Rightarrow\mathrm{z}=\pm\frac{\mathrm{3}}{\mathrm{2}}}\end{cases} \\ $$
Commented by TawaTawa last updated on 20/Jan/20
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *