Menu Close

p-n-1-1-n-2-1-2-n-2-1-n-n-2-k-1-n-k-2-1-6-n-2n-1-n-1-show-that-1-2-1-1-n-1-12n-2-2n-1-n-1-lt-ln-p-n-lt-1-2-1-1-n-hence-find-lim-n-p-n-2-show-that

Tinku Tara 0 Comments
Pin




Question Number 144483 by alcohol last updated on 25/Jun/21
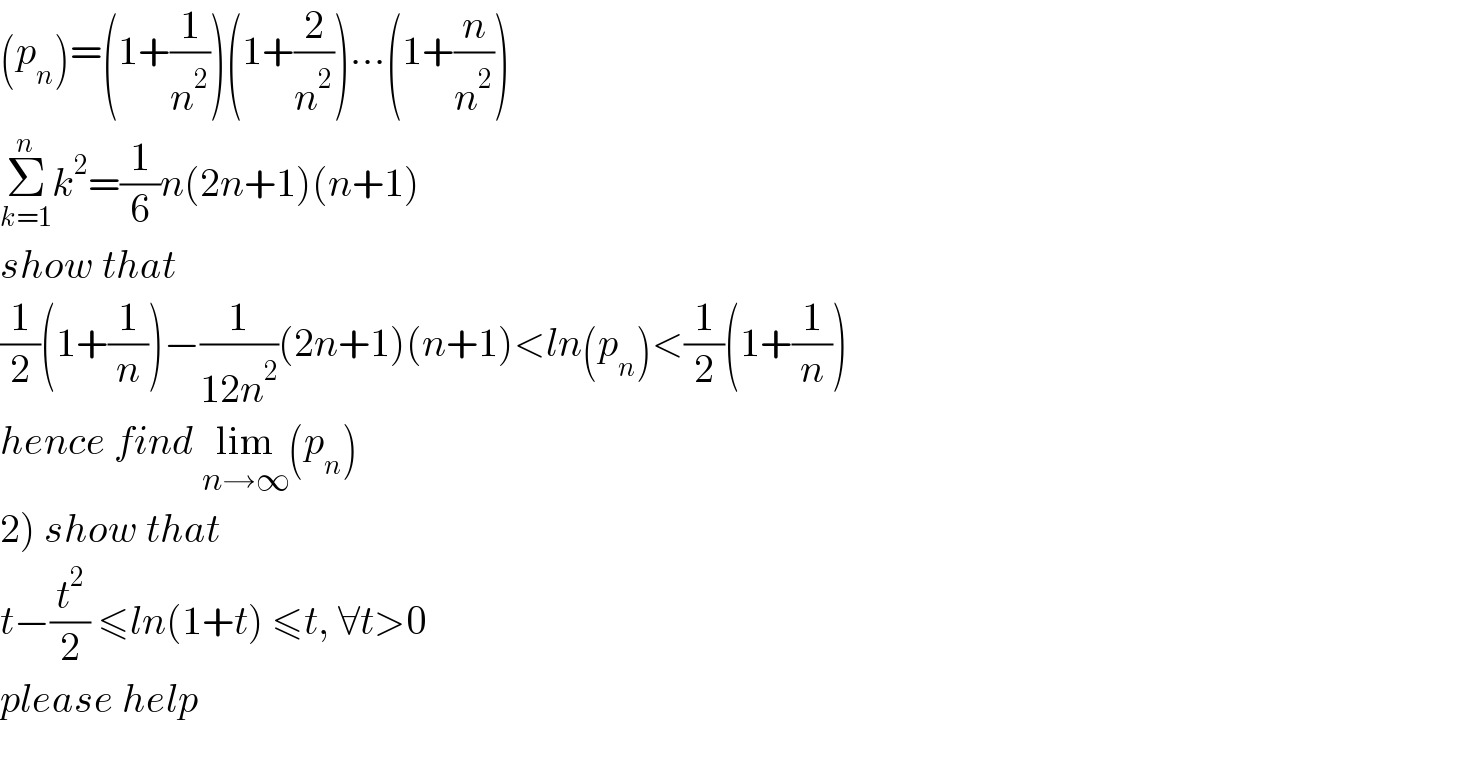
(p_n )=(1+(1/n^2 ))(1+(2/n^2 ))...(1+(n/n^2 )) Σ_(k=1) ^n k^2 =(1/6)n(2n+1)(n+1) show that (1/2)(1+(1/n))−(1/(12n^2 ))(2n+1)(n+1)<ln(p_n )<(1/2)(1+(1/n)) hence find lim_(n→∞) (p_n ) 2) show that t−(t^2 /2) ≤ln(1+t) ≤t, ∀t>0 please help
$$\left({p}_{{n}} \right)=\left(\mathrm{1}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{\mathrm{2}}{{n}^{\mathrm{2}} }\right)…\left(\mathrm{1}+\frac{{n}}{{n}^{\mathrm{2}} }\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}{n}\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right) \\ $$$${show}\:{that} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)−\frac{\mathrm{1}}{\mathrm{12}{n}^{\mathrm{2}} }\left(\mathrm{2}{n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)<{ln}\left({p}_{{n}} \right)<\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$$${hence}\:{find}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left({p}_{{n}} \right) \\ $$$$\left.\mathrm{2}\right)\:{show}\:{that}\: \\ $$$${t}−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}\:\leqslant{ln}\left(\mathrm{1}+{t}\right)\:\leqslant{t},\:\forall{t}>\mathrm{0} \\ $$$${please}\:{help} \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 26/Jun/21
ln(1+x) = Σ_(n=0) ^∞ (−1)^n (x^(n+1) /(n+1)) ⇒ x−(x^2 /2) < ln(1+x) < x (1) p_n = Π_(k=1) ^n (1+(k/n^2 )) lnp_n = Σ_(k=1) ^n ln(1+(k/n^2 )) (1) : (k/n^2 )−(k^2 /(2n^4 )) < ln(1+(k/n^2 )) < (k/n^2 ) Σ_(k=1) ^n ((k/n^2 )−(k^2 /(2n^4 ))) < lnp_n =Σ_(k=1) ^n ln(1+(k/n^2 )) <Σ_(k=1) ^n (k/n^2 ) ((n(n+1))/(2n^2 ))−((n(n+1)(2n+1))/(12n^4 )) < p_n < ((n(n+1))/(2n^2 )) (1/2)(1+(1/n))−(((n+1)(2n+1))/(12n^3 )) < p_n < (1/2)(1+(1/n))
$$\mathrm{ln}\left(\mathrm{1}+{x}\right)\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:<\:\mathrm{ln}\left(\mathrm{1}+{x}\right)\:<\:{x}\:\:\:\:\left(\mathrm{1}\right) \\ $$$${p}_{{n}} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{ln}{p}_{{n}} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\left(\mathrm{1}\right)\::\:\frac{{k}}{{n}^{\mathrm{2}} }−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:<\:\mathrm{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:<\:\frac{{k}}{{n}^{\mathrm{2}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{{k}}{{n}^{\mathrm{2}} }−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\right)\:<\:\mathrm{ln}{p}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:<\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{{n}^{\mathrm{2}} } \\ $$$$\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} }−\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{4}} }\:<\:{p}_{{n}} \:<\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}{n}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)−\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{3}} }\:<\:{p}_{{n}} \:<\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right) \\ $$
Commented by alcohol last updated on 26/Jun/21
thank you brother
$${thank}\:{you}\:{brother} \\ $$
Commented by puissant last updated on 07/Jul/21
Desole mais il ya erreur c′est ln(p_n ) qui est encadre^� .. ainsi lim_(n→+∞) ln(p_n )=(1/2) donc lim_(n→+∞) (p_n )=(√e).
$$\mathrm{Desole}\:\mathrm{mais}\:\mathrm{il}\:\mathrm{ya}\:\mathrm{erreur}\:\mathrm{c}'\mathrm{est}\:\mathrm{ln}\left(\mathrm{p}_{\mathrm{n}} \right)\:\mathrm{qui} \\ $$$$\mathrm{est}\:\mathrm{encadr}\acute {\mathrm{e}}.. \\ $$$$\mathrm{ainsi}\:\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{p}_{\mathrm{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{donc}\:\:\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \left(\mathrm{p}_{\mathrm{n}} \right)=\sqrt{\mathrm{e}}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *