Question-79026

Question Number 79026 by TawaTawa last updated on 22/Jan/20

Commented by mathmax by abdo last updated on 22/Jan/20

we consider the repere (D,DC^→ ,DA^→ ) ⇒D(0,0) ,C(1,0) A(0,1) (1=20cm) ⇒B(1,1) and F((1/2),1) coordonnate of I? M(x,y) ∈ (CF) ⇒det(CM^→ ,CF^→ )=0 ⇒ determinant (((x−1 −(1/2))),((y 1)))=0⇒ (x−1)+(1/2)y=0 ⇒2x−2+y =0 ⇒2x+y−2=0 equation of (BE) E(0,(1/2)) M(x,y) ∈(BE) ⇒det(BM^→ ,BE^→ )=0 ⇒ determinant (((x−1 −1)),((y−1 −(1/2))))=0 ⇒ −(1/2)(x−1)+y−1=0 ⇒(1/2)(x−1)−y+1=0 ⇒x−1−2y+2=0 ⇒ x−2y+1=0 let solve the systeme { ((2x+y−2=0)),((x−2y+1=0 )) :} ⇒ { ((y=−2x+2)),((x−2(−2x+2)+1=0 ⇒ { ((y=−2x+2)),((5x−3=0 ⇒)) :})) :} { ((x=(3/5) ⇒ { ((x=(3/5))),((y=(4/5))) :})),((y=−(6/5)+2 )) :} ⇒ I((3/5),(4/5)) A(BIF)=(1/2)∣det(IF^→ ,IB^→ ) we have IF^→ ((1/2)−(3/5),1−(4/5)) ⇒IF^→ (−(1/(10)),(1/5)) and IB^→ (1−(3/5),1−(4/5)) ⇒IB^→ ((2/5),(1/5)) ⇒ A(BIF) =(1/2)∣ determinant (((−(1/(10)) (2/5))),(((1/5) (1/5))))∣=(1/2)∣(−(1/(50))−(2/(25)))∣ =(1/2)×(5/(50)) =(1/(20)) we have 1 =20 cm ⇒1^2 =20^2 cm^2 ⇒ A(BIF) =(1/(20))×20^2 =20 cm^2 .

$${we}\:{consider}\:{the}\:{repere}\:\left({D},{D}\overset{\rightarrow} {{C}},{D}\overset{\rightarrow} {{A}}\right)\:\Rightarrow{D}\left(\mathrm{0},\mathrm{0}\right)\:,{C}\left(\mathrm{1},\mathrm{0}\right)\:{A}\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\left(\mathrm{1}=\mathrm{20}{cm}\right)\:\Rightarrow{B}\left(\mathrm{1},\mathrm{1}\right)\:\:{and}\:{F}\left(\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}\right)\:\:{coordonnate}\:{of}\:{I}? \\ $$$${M}\left({x},{y}\right)\:\in\:\left({CF}\right)\:\Rightarrow{det}\left({C}\overset{\rightarrow} {{M}},{C}\overset{\rightarrow} {{F}}\right)=\mathrm{0}\:\Rightarrow\begin{vmatrix}{{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\\{{y}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{vmatrix}=\mathrm{0}\Rightarrow \\ $$$$\left({x}−\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{2}}{y}=\mathrm{0}\:\Rightarrow\mathrm{2}{x}−\mathrm{2}+{y}\:=\mathrm{0}\:\Rightarrow\mathrm{2}{x}+{y}−\mathrm{2}=\mathrm{0} \\ $$$${equation}\:{of}\:\left({BE}\right)\:\:\:{E}\left(\mathrm{0},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${M}\left({x},{y}\right)\:\in\left({BE}\right)\:\Rightarrow{det}\left({B}\overset{\rightarrow} {{M}}\:,{B}\overset{\rightarrow} {{E}}\right)=\mathrm{0}\:\Rightarrow\begin{vmatrix}{{x}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{{y}−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}}}\end{vmatrix}=\mathrm{0}\:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{1}\right)+{y}−\mathrm{1}=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\mathrm{1}\right)−{y}+\mathrm{1}=\mathrm{0}\:\Rightarrow{x}−\mathrm{1}−\mathrm{2}{y}+\mathrm{2}=\mathrm{0}\:\Rightarrow \\ $$$${x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:\:\:{let}\:{solve}\:{the}\:{systeme}\:\begin{cases}{\mathrm{2}{x}+{y}−\mathrm{2}=\mathrm{0}}\\{{x}−\mathrm{2}{y}+\mathrm{1}=\mathrm{0}\:}\end{cases} \\ $$$$\:\:\:\:\Rightarrow\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{2}}\\{{x}−\mathrm{2}\left(−\mathrm{2}{x}+\mathrm{2}\right)+\mathrm{1}=\mathrm{0}\:\Rightarrow\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{2}}\\{\mathrm{5}{x}−\mathrm{3}=\mathrm{0}\:\Rightarrow}\end{cases}}\end{cases} \\ $$$$\begin{cases}{{x}=\frac{\mathrm{3}}{\mathrm{5}}\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\begin{cases}{{x}=\frac{\mathrm{3}}{\mathrm{5}}}\\{{y}=\frac{\mathrm{4}}{\mathrm{5}}}\end{cases}}\\{{y}=−\frac{\mathrm{6}}{\mathrm{5}}+\mathrm{2}\:}\end{cases} \\ $$$$\Rightarrow\:{I}\left(\frac{\mathrm{3}}{\mathrm{5}},\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$${A}\left({BIF}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mid{det}\left({I}\overset{\rightarrow} {{F}},{I}\overset{\rightarrow} {{B}}\right)\:\:\:\:\:{we}\:{have}\:{I}\overset{\rightarrow} {{F}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\Rightarrow{I}\overset{\rightarrow} {{F}}\left(−\frac{\mathrm{1}}{\mathrm{10}},\frac{\mathrm{1}}{\mathrm{5}}\right)\:\:\:\:{and}\:{I}\overset{\rightarrow} {{B}}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}},\mathrm{1}−\frac{\mathrm{4}}{\mathrm{5}}\right)\:\Rightarrow{I}\overset{\rightarrow} {{B}}\left(\frac{\mathrm{2}}{\mathrm{5}},\frac{\mathrm{1}}{\mathrm{5}}\right)\:\Rightarrow \\ $$$${A}\left({BIF}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\mid\begin{vmatrix}{−\frac{\mathrm{1}}{\mathrm{10}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{5}}}\\{\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{5}}}\end{vmatrix}\mid=\frac{\mathrm{1}}{\mathrm{2}}\mid\left(−\frac{\mathrm{1}}{\mathrm{50}}−\frac{\mathrm{2}}{\mathrm{25}}\right)\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{5}}{\mathrm{50}}\:=\frac{\mathrm{1}}{\mathrm{20}}\:\:\:\:\:\:{we}\:{have}\:\mathrm{1}\:=\mathrm{20}\:{cm}\:\Rightarrow\mathrm{1}^{\mathrm{2}} =\mathrm{20}^{\mathrm{2}} {cm}^{\mathrm{2}} \:\Rightarrow \\ $$$${A}\left({BIF}\right)\:=\frac{\mathrm{1}}{\mathrm{20}}×\mathrm{20}^{\mathrm{2}} \:=\mathrm{20}\:{cm}^{\mathrm{2}} . \\ $$

Commented by TawaTawa last updated on 22/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by msup trace by abdo last updated on 22/Jan/20

$${you}\:{are}\:{welcome} \\ $$

Commented by jagoll last updated on 22/Jan/20

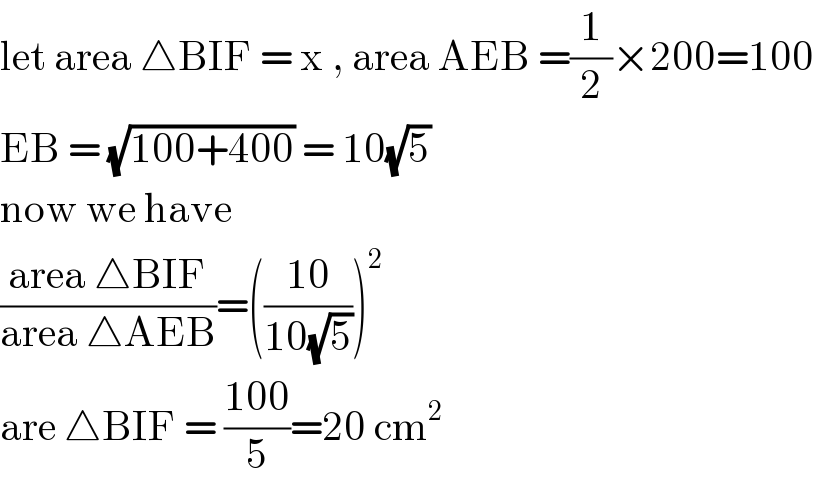
let area △BIF = x , area AEB =(1/2)×200=100 EB = (√(100+400)) = 10(√5) now we have ((area △BIF)/(area △AEB))=(((10)/(10(√5))))^2 are △BIF = ((100)/5)=20 cm^(2 )

$$\mathrm{let}\:\mathrm{area}\:\bigtriangleup\mathrm{BIF}\:=\:\mathrm{x}\:,\:\mathrm{area}\:\mathrm{AEB}\:=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{200}=\mathrm{100} \\ $$$$\mathrm{EB}\:=\:\sqrt{\mathrm{100}+\mathrm{400}}\:=\:\mathrm{10}\sqrt{\mathrm{5}} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\frac{\mathrm{area}\:\bigtriangleup\mathrm{BIF}}{\mathrm{area}\:\bigtriangleup\mathrm{AEB}}=\left(\frac{\mathrm{10}}{\mathrm{10}\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} \\ $$$$\mathrm{are}\:\bigtriangleup\mathrm{BIF}\:=\:\frac{\mathrm{100}}{\mathrm{5}}=\mathrm{20}\:\mathrm{cm}^{\mathrm{2}\:} \\ $$

Commented by TawaTawa last updated on 23/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mind is power last updated on 22/Jan/20

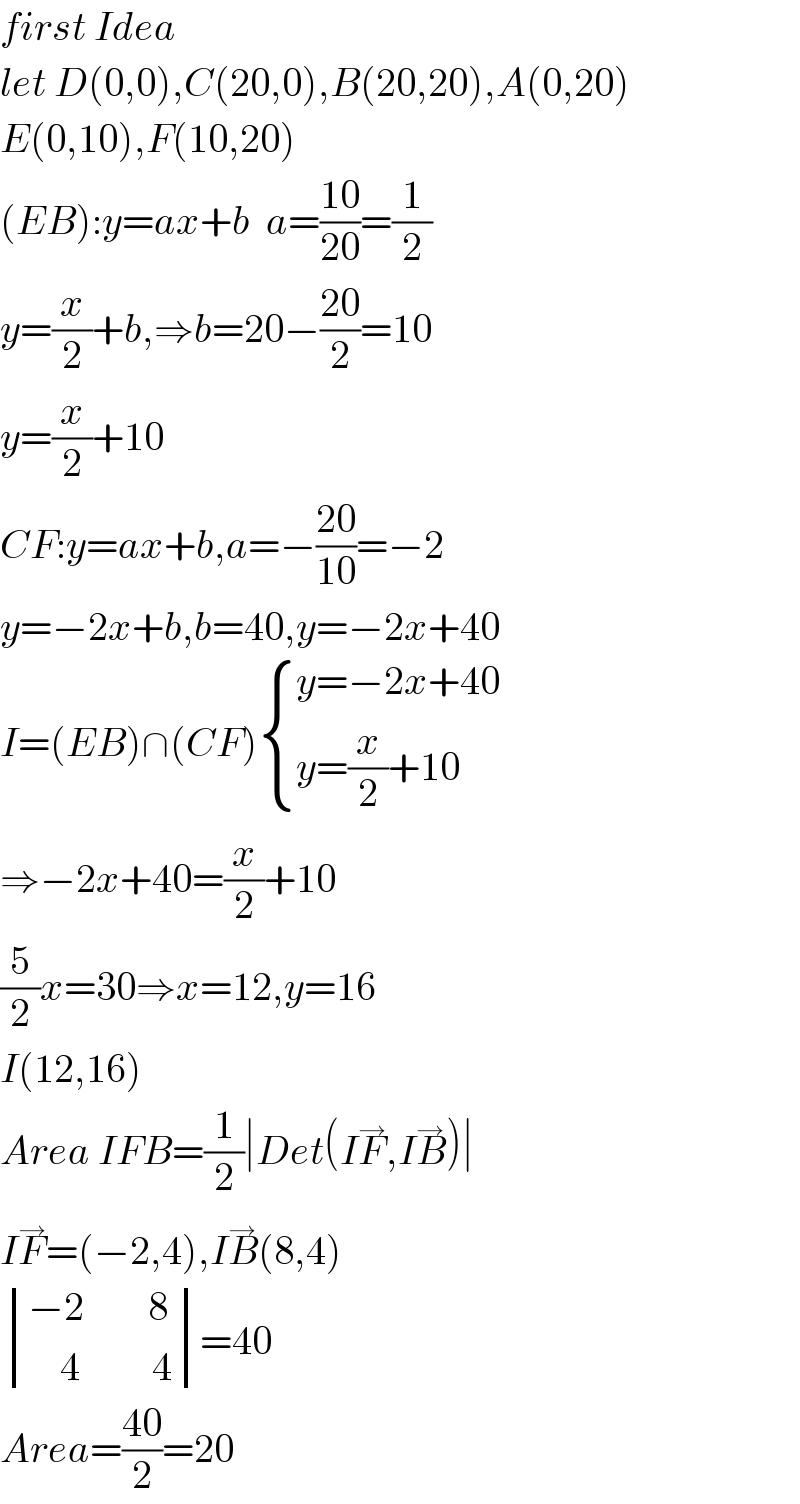
first Idea let D(0,0),C(20,0),B(20,20),A(0,20) E(0,10),F(10,20) (EB):y=ax+b a=((10)/(20))=(1/2) y=(x/2)+b,⇒b=20−((20)/2)=10 y=(x/2)+10 CF:y=ax+b,a=−((20)/(10))=−2 y=−2x+b,b=40,y=−2x+40 I=(EB)∩(CF) { ((y=−2x+40)),((y=(x/2)+10)) :} ⇒−2x+40=(x/2)+10 (5/2)x=30⇒x=12,y=16 I(12,16) Area IFB=(1/2)∣Det(IF^→ ,IB^→ )∣ IF^→ =(−2,4),IB^→ (8,4) determinant (((−2 8)),(( 4 4)))=40 Area=((40)/2)=20

$${first}\:{Idea} \\ $$$${let}\:{D}\left(\mathrm{0},\mathrm{0}\right),{C}\left(\mathrm{20},\mathrm{0}\right),{B}\left(\mathrm{20},\mathrm{20}\right),{A}\left(\mathrm{0},\mathrm{20}\right) \\ $$$${E}\left(\mathrm{0},\mathrm{10}\right),{F}\left(\mathrm{10},\mathrm{20}\right) \\ $$$$\left({EB}\right):{y}={ax}+{b}\:\:{a}=\frac{\mathrm{10}}{\mathrm{20}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+{b},\Rightarrow{b}=\mathrm{20}−\frac{\mathrm{20}}{\mathrm{2}}=\mathrm{10} \\ $$$${y}=\frac{{x}}{\mathrm{2}}+\mathrm{10} \\ $$$${CF}:{y}={ax}+{b},{a}=−\frac{\mathrm{20}}{\mathrm{10}}=−\mathrm{2} \\ $$$${y}=−\mathrm{2}{x}+{b},{b}=\mathrm{40},{y}=−\mathrm{2}{x}+\mathrm{40} \\ $$$${I}=\left({EB}\right)\cap\left({CF}\right)\begin{cases}{{y}=−\mathrm{2}{x}+\mathrm{40}}\\{{y}=\frac{{x}}{\mathrm{2}}+\mathrm{10}}\end{cases} \\ $$$$\Rightarrow−\mathrm{2}{x}+\mathrm{40}=\frac{{x}}{\mathrm{2}}+\mathrm{10} \\ $$$$\frac{\mathrm{5}}{\mathrm{2}}{x}=\mathrm{30}\Rightarrow{x}=\mathrm{12},{y}=\mathrm{16} \\ $$$${I}\left(\mathrm{12},\mathrm{16}\right) \\ $$$${Area}\:{IFB}=\frac{\mathrm{1}}{\mathrm{2}}\mid{Det}\left({I}\overset{\rightarrow} {{F}},{I}\overset{\rightarrow} {{B}}\right)\mid \\ $$$${I}\overset{\rightarrow} {{F}}=\left(−\mathrm{2},\mathrm{4}\right),{I}\overset{\rightarrow} {{B}}\left(\mathrm{8},\mathrm{4}\right) \\ $$$$\begin{vmatrix}{−\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{8}}\\{\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{4}}\end{vmatrix}=\mathrm{40} \\ $$$${Area}=\frac{\mathrm{40}}{\mathrm{2}}=\mathrm{20} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 22/Jan/20

Commented by mr W last updated on 22/Jan/20

FG=((AE)/2)=((AD)/4)=((BC)/4) ((HB)/(FB−HB))=((HB)/(FH))=((BC)/(FG))=4 ⇒HB=(4/5)FB=IK ⇒Δ_(IBC) =(4/5)Δ_(FBC) ⇒Δ_(BIF) =Δ_(FBC) −Δ_(IBC) =(1/5)Δ_(FBC) =(1/5)×(([ABCD])/4) =((20×20)/(20))=20 cm^2

$${FG}=\frac{{AE}}{\mathrm{2}}=\frac{{AD}}{\mathrm{4}}=\frac{{BC}}{\mathrm{4}} \\ $$$$\frac{{HB}}{{FB}−{HB}}=\frac{{HB}}{{FH}}=\frac{{BC}}{{FG}}=\mathrm{4} \\ $$$$\Rightarrow{HB}=\frac{\mathrm{4}}{\mathrm{5}}{FB}={IK} \\ $$$$\Rightarrow\Delta_{{IBC}} =\frac{\mathrm{4}}{\mathrm{5}}\Delta_{{FBC}} \\ $$$$\Rightarrow\Delta_{{BIF}} =\Delta_{{FBC}} −\Delta_{{IBC}} =\frac{\mathrm{1}}{\mathrm{5}}\Delta_{{FBC}} =\frac{\mathrm{1}}{\mathrm{5}}×\frac{\left[{ABCD}\right]}{\mathrm{4}} \\ $$$$=\frac{\mathrm{20}×\mathrm{20}}{\mathrm{20}}=\mathrm{20}\:{cm}^{\mathrm{2}} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

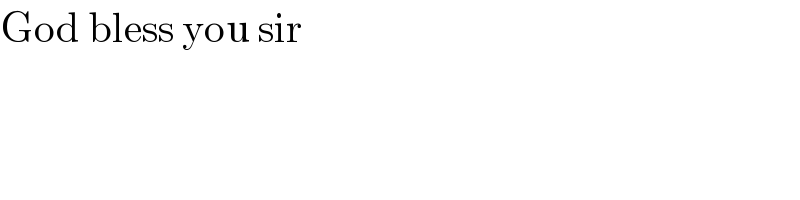
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by john santu last updated on 22/Jan/20

Commented by TawaTawa last updated on 22/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 22/Jan/20

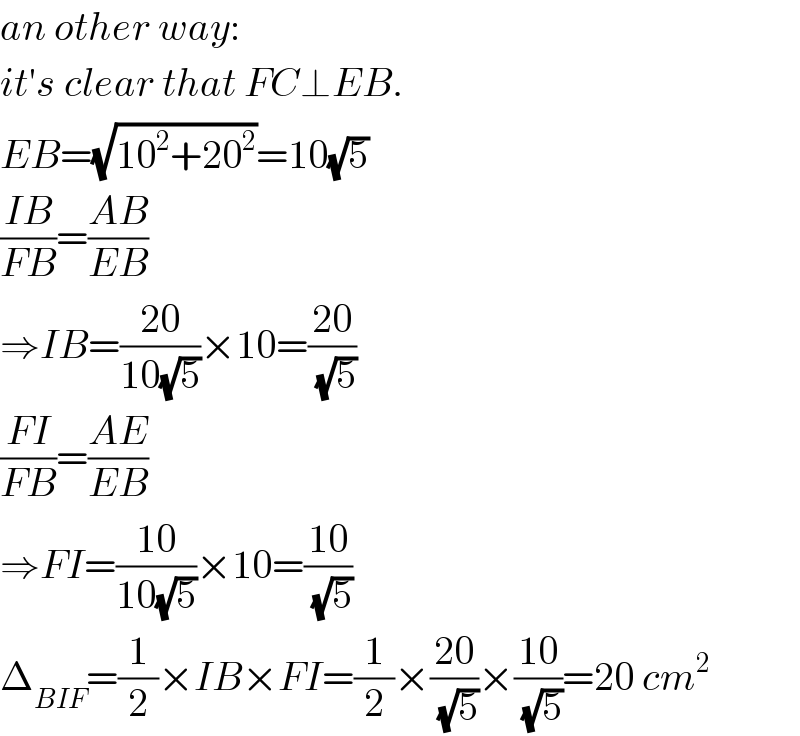
an other way: it′s clear that FC⊥EB. EB=(√(10^2 +20^2 ))=10(√5) ((IB)/(FB))=((AB)/(EB)) ⇒IB=((20)/(10(√5)))×10=((20)/( (√5))) ((FI)/(FB))=((AE)/(EB)) ⇒FI=((10)/(10(√5)))×10=((10)/( (√5))) Δ_(BIF) =(1/2)×IB×FI=(1/2)×((20)/( (√5)))×((10)/( (√5)))=20 cm^2

$${an}\:{other}\:{way}: \\ $$$${it}'{s}\:{clear}\:{that}\:{FC}\bot{EB}. \\ $$$${EB}=\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{20}^{\mathrm{2}} }=\mathrm{10}\sqrt{\mathrm{5}} \\ $$$$\frac{{IB}}{{FB}}=\frac{{AB}}{{EB}} \\ $$$$\Rightarrow{IB}=\frac{\mathrm{20}}{\mathrm{10}\sqrt{\mathrm{5}}}×\mathrm{10}=\frac{\mathrm{20}}{\:\sqrt{\mathrm{5}}} \\ $$$$\frac{{FI}}{{FB}}=\frac{{AE}}{{EB}} \\ $$$$\Rightarrow{FI}=\frac{\mathrm{10}}{\mathrm{10}\sqrt{\mathrm{5}}}×\mathrm{10}=\frac{\mathrm{10}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Delta_{{BIF}} =\frac{\mathrm{1}}{\mathrm{2}}×{IB}×{FI}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{20}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{10}}{\:\sqrt{\mathrm{5}}}=\mathrm{20}\:{cm}^{\mathrm{2}} \\ $$

Commented by TawaTawa last updated on 22/Jan/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply