Question Number 13498 by sin (x) last updated on 20/May/17
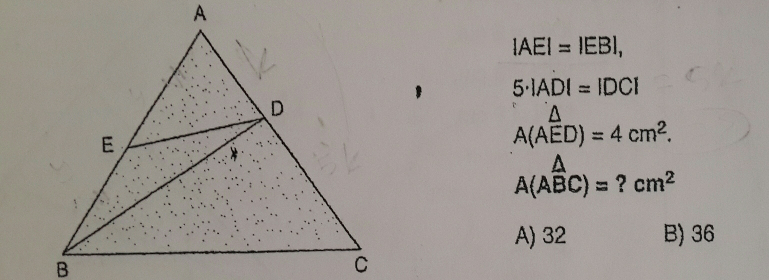
Commented by ajfour last updated on 20/May/17
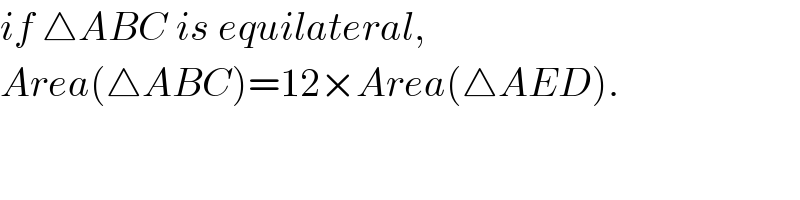
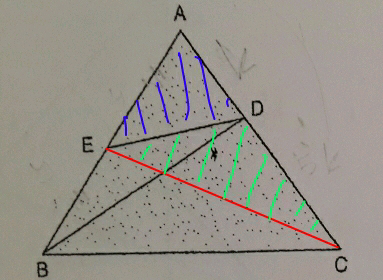
$${if}\:\bigtriangleup{ABC}\:{is}\:{equilateral}, \\ $$$${Area}\left(\bigtriangleup{ABC}\right)=\mathrm{12}×{Area}\left(\bigtriangleup{AED}\right). \\ $$
Answered by mrW1 last updated on 21/May/17
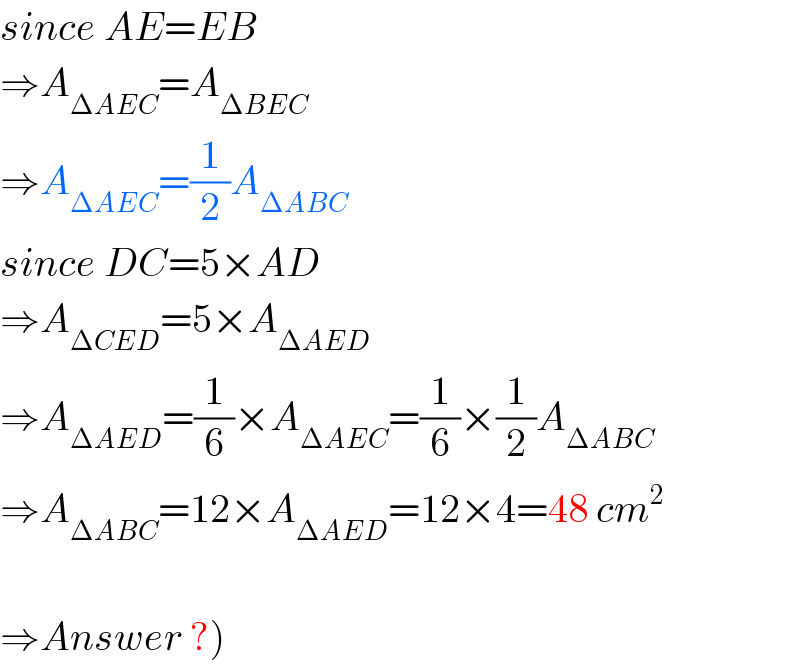
$${since}\:{AE}={EB} \\ $$$$\Rightarrow{A}_{\Delta{AEC}} ={A}_{\Delta{BEC}} \\ $$$$\Rightarrow{A}_{\Delta{AEC}} =\frac{\mathrm{1}}{\mathrm{2}}{A}_{\Delta{ABC}} \\ $$$${since}\:{DC}=\mathrm{5}×{AD} \\ $$$$\Rightarrow{A}_{\Delta{CED}} =\mathrm{5}×{A}_{\Delta{AED}} \\ $$$$\Rightarrow{A}_{\Delta{AED}} =\frac{\mathrm{1}}{\mathrm{6}}×{A}_{\Delta{AEC}} =\frac{\mathrm{1}}{\mathrm{6}}×\frac{\mathrm{1}}{\mathrm{2}}{A}_{\Delta{ABC}} \\ $$$$\Rightarrow{A}_{\Delta{ABC}} =\mathrm{12}×{A}_{\Delta{AED}} =\mathrm{12}×\mathrm{4}=\mathrm{48}\:{cm}^{\mathrm{2}} \\ $$$$ \\ $$$$\left.\Rightarrow{Answer}\:?\right) \\ $$
Commented by mrW1 last updated on 21/May/17
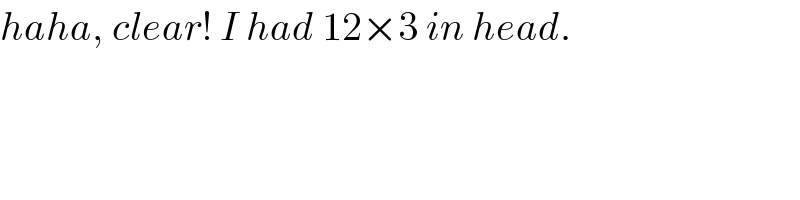
$${haha},\:{clear}!\:{I}\:{had}\:\mathrm{12}×\mathrm{3}\:{in}\:{head}. \\ $$
Commented by mrW1 last updated on 21/May/17
Commented by ajfour last updated on 21/May/17

$$\mathrm{12}×\mathrm{4}\neq\mathrm{36}\:. \\ $$
Commented by ajfour last updated on 21/May/17

$$\mathrm{i}\:\mathrm{understand}\:. \\ $$
