Question Number 79079 by ketto255 last updated on 22/Jan/20
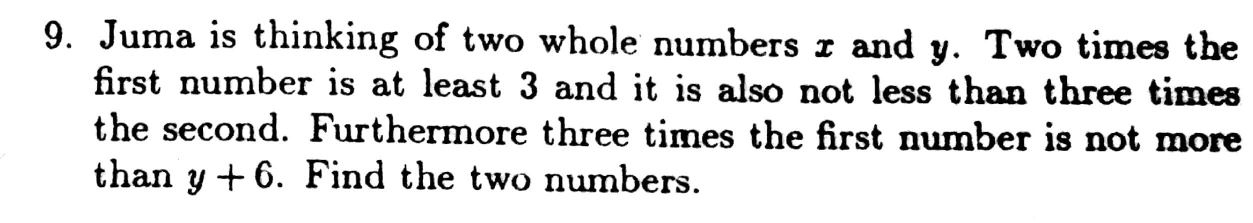
Answered by mr W last updated on 22/Jan/20
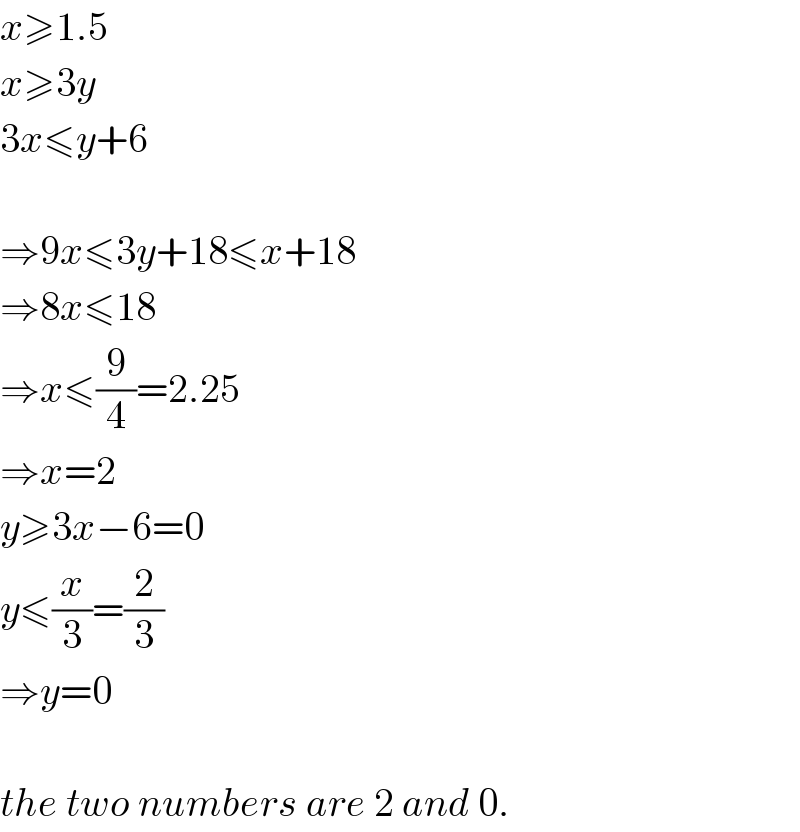
$${x}\geqslant\mathrm{1}.\mathrm{5} \\ $$$${x}\geqslant\mathrm{3}{y} \\ $$$$\mathrm{3}{x}\leqslant{y}+\mathrm{6} \\ $$$$ \\ $$$$\Rightarrow\mathrm{9}{x}\leqslant\mathrm{3}{y}+\mathrm{18}\leqslant{x}+\mathrm{18} \\ $$$$\Rightarrow\mathrm{8}{x}\leqslant\mathrm{18} \\ $$$$\Rightarrow{x}\leqslant\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{2}.\mathrm{25} \\ $$$$\Rightarrow{x}=\mathrm{2} \\ $$$${y}\geqslant\mathrm{3}{x}−\mathrm{6}=\mathrm{0} \\ $$$${y}\leqslant\frac{{x}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{y}=\mathrm{0} \\ $$$$ \\ $$$${the}\:{two}\:{numbers}\:{are}\:\mathrm{2}\:{and}\:\mathrm{0}. \\ $$
