Question Number 144622 by phally last updated on 27/Jun/21

Answered by alcohol last updated on 27/Jun/21

$${e}^{\frac{\mathrm{1}}{\mathrm{2}{a}}} \\ $$
Answered by mathmax by abdo last updated on 27/Jun/21
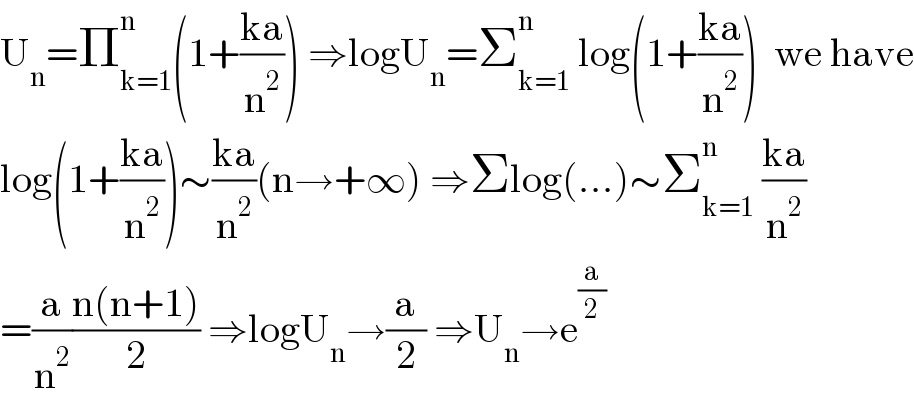
$$\mathrm{U}_{\mathrm{n}} =\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{1}+\frac{\mathrm{ka}}{\mathrm{n}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{logU}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{ka}}{\mathrm{n}^{\mathrm{2}} }\right)\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{log}\left(\mathrm{1}+\frac{\mathrm{ka}}{\mathrm{n}^{\mathrm{2}} }\right)\sim\frac{\mathrm{ka}}{\mathrm{n}^{\mathrm{2}} }\left(\mathrm{n}\rightarrow+\infty\right)\:\Rightarrow\Sigma\mathrm{log}\left(…\right)\sim\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{ka}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{a}}{\mathrm{n}^{\mathrm{2}} }\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}{\mathrm{2}}\:\Rightarrow\mathrm{logU}_{\mathrm{n}} \rightarrow\frac{\mathrm{a}}{\mathrm{2}}\:\Rightarrow\mathrm{U}_{\mathrm{n}} \rightarrow\mathrm{e}^{\frac{\mathrm{a}}{\mathrm{2}}} \\ $$
Commented by phally last updated on 27/Jun/21

$${thank}\:{brother} \\ $$
Commented by mathmax by abdo last updated on 27/Jun/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
