Question Number 79102 by mathmax by abdo last updated on 22/Jan/20
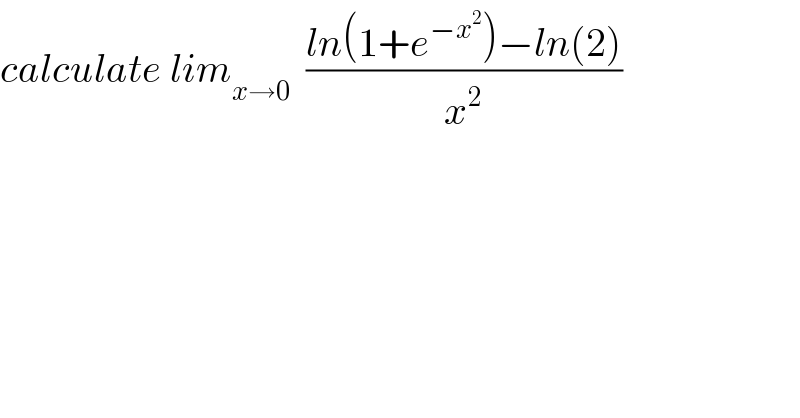
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)−{ln}\left(\mathrm{2}\right)}{{x}^{\mathrm{2}} } \\ $$
Commented by mathmax by abdo last updated on 24/Jan/20
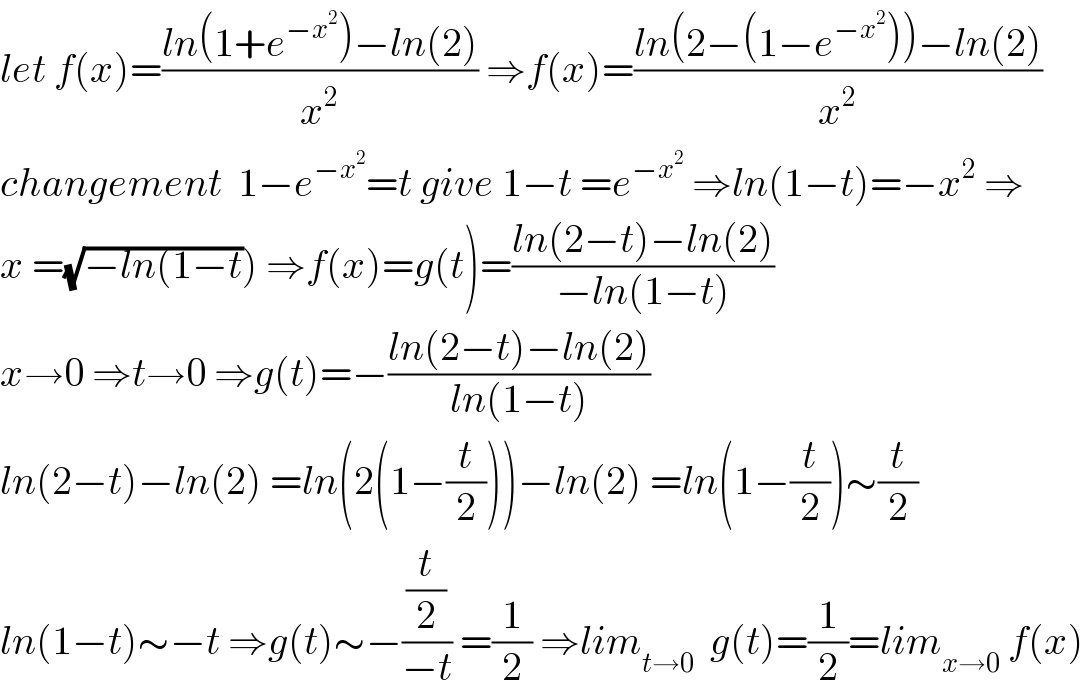
$${let}\:{f}\left({x}\right)=\frac{{ln}\left(\mathrm{1}+{e}^{−{x}^{\mathrm{2}} } \right)−{ln}\left(\mathrm{2}\right)}{{x}^{\mathrm{2}} }\:\Rightarrow{f}\left({x}\right)=\frac{{ln}\left(\mathrm{2}−\left(\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } \right)\right)−{ln}\left(\mathrm{2}\right)}{{x}^{\mathrm{2}} } \\ $$$${changement}\:\:\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } ={t}\:{give}\:\mathrm{1}−{t}\:={e}^{−{x}^{\mathrm{2}} } \:\Rightarrow{ln}\left(\mathrm{1}−{t}\right)=−{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\left.{x}\:=\sqrt{−{ln}\left(\mathrm{1}−{t}\right.}\right)\:\Rightarrow{f}\left({x}\right)={g}\left({t}\right)=\frac{{ln}\left(\mathrm{2}−{t}\right)−{ln}\left(\mathrm{2}\right)}{−{ln}\left(\mathrm{1}−{t}\right)} \\ $$$${x}\rightarrow\mathrm{0}\:\Rightarrow{t}\rightarrow\mathrm{0}\:\Rightarrow{g}\left({t}\right)=−\frac{{ln}\left(\mathrm{2}−{t}\right)−{ln}\left(\mathrm{2}\right)}{{ln}\left(\mathrm{1}−{t}\right)} \\ $$$${ln}\left(\mathrm{2}−{t}\right)−{ln}\left(\mathrm{2}\right)\:={ln}\left(\mathrm{2}\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right)\right)−{ln}\left(\mathrm{2}\right)\:={ln}\left(\mathrm{1}−\frac{{t}}{\mathrm{2}}\right)\sim\frac{{t}}{\mathrm{2}} \\ $$$${ln}\left(\mathrm{1}−{t}\right)\sim−{t}\:\Rightarrow{g}\left({t}\right)\sim−\frac{\frac{{t}}{\mathrm{2}}}{−{t}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow{lim}_{{t}\rightarrow\mathrm{0}} \:\:{g}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{2}}={lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right) \\ $$
