∫_0 ^1 logxlog(1−x)dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 103154 by Dwaipayan Shikari last updated on 13/Jul/20

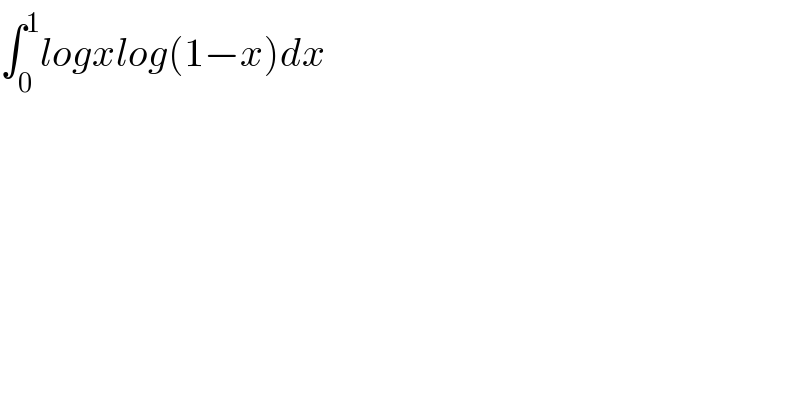
$\int_{0}^{1} l o g x l o g (1 - x) d x$
	Answered by OlafThorendsen last updated on 13/Jul/20

	$I = \int_{0}^{1} \ln x \ln (1 - x) d x$ $- \frac{1}{1 - x} = - \underset{n = 0}{\sum^{\infty}} x^{n}$ $\ln (1 - x) = - \underset{n = 0}{\sum^{\infty}} \frac{x^{n + 1}}{n + 1} = - \underset{n = 1}{\sum^{\infty}} \frac{x^{n}}{n}$ $I = - \int_{0}^{1} \ln x \underset{n = 1}{\sum^{\infty}} \frac{x^{n}}{n} d x$ $I = - \underset{n = 1}{\sum^{\infty}} \frac{1}{n} \int_{0}^{1} x^{n} \ln x d x$ $I_{n} = - \int_{0}^{1} x^{n} \ln x d x$ $I_{n} = - {[\frac{x^{n + 1}}{n + 1} \ln x]}_{0}^{1} + \int_{0}^{1} \frac{x^{n + 1}}{n + 1} . \frac{1}{x} d x$ $I_{n} = 0 + \int_{0}^{1} \frac{x^{n}}{n + 1} d x = {[\frac{x^{n + 1}}{{(n + 1)}^{2}}]}_{0}^{1}$ $I_{n} = \frac{1}{{(n + 1)}^{2}}$ $I = \underset{n = 1}{\sum^{\infty}} \frac{1}{n} I_{n} = \underset{n = 1}{\sum^{\infty}} \frac{1}{n {(n + 1)}^{2}}$ $I = \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + 1} - \frac{1}{{(n + 1)}^{2}})$ $\underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + 1}) = (1 - \frac{1}{2}) + (\frac{1}{2} - \frac{1}{3}) + . . .$ $\underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + 1}) = 1$ $I = 1 - \underset{n = 1}{\sum^{\infty}} \frac{1}{{(n + 1)}^{2}}$ $I = 1 - \underset{n = 2}{\sum^{\infty}} \frac{1}{n^{2}}$ $I = 2 - \underset{n = 1}{\sum^{\infty}} \frac{1}{n^{2}}$ $I = 2 - ζ (2) = 2 - \frac{π^{2}}{6}$
	Commented by Dwaipayan Shikari last updated on 13/Jul/20

	$G r e a t s i r!$
	Answered by bobhans last updated on 13/Jul/20
	$I = ∫_0 ^1 ln(x) ln(1−x) dx by Maclaurin series ln(1−x) = −Σ_(n=1) ^∞ (x^n /n) we obtain I=−∫_0 ^1 ln(x)Σ_(n=1) ^∞ (x^n /n) dx I = −Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^n ln(x) dx [ by parts ] { ((u = ln(x))),((dv = x^n dx )) :} I=−Σ_(n=1) ^∞ (1/n)∣((x^(n+1) /(n+1)) ln(x)−(x^(n+1) /((n+1)^2 )))∣_0 ^1 I= Σ_(n=1) ^∞ (1/(n(n+1)^2 )) [ by L′Hopital rule′s] I= Σ_(n=1) ^∞ ((1/n)−(1/(n+1))−(1/((n+1)^2 ))) the first series Σ_(n=1) ^∞ ((1/n)−(1/(n+1))) is telescoping ⇒ lim_(p→∞) Σ_(n=1) ^p ((1/n)−(1/(n+1))) = lim_(p→∞) (1−(1/(p+1))) = 1 now the second series Σ_(n=1) ^∞ (1/((n+1)^2 )) = Σ_(k=2) ^∞ (1/k^2 ) = −1+Σ_(k=1) ^∞ (1/k^2 ) = −1+(π^2 /6) . therefore I = ∫_0 ^1 ln(x) ln(1−x)dx = 1−(−1+(π^2 /6)) = 2−(π^2 /6) . ★$
	$I = \underset{0}{\int^{1}} \ln (x) \ln (1 - x) d x$ $b y M a c l a u r i n s e r i e s$ $\ln (1 - x) = - \underset{n = 1}{\sum^{\infty}} \frac{x^{n}}{n}$ $w e o b t a i n I = - \underset{0}{\int^{1}} \ln (x) \underset{n = 1}{\sum^{\infty}} \frac{x^{n}}{n} d x$ $I = - \underset{n = 1}{\sum^{\infty}} \frac{1}{n} \underset{0}{\int^{1}} x^{n} \ln (x) d x [b y p a r t s]$ ${\begin{cases} u = \ln (x) \\ d v = x^{n} d x \end{cases}$ $I = - \underset{n = 1}{\sum^{\infty}} \frac{1}{n} ∣ (\frac{x^{n + 1}}{n + 1} \ln (x) - \frac{x^{n + 1}}{{(n + 1)}^{2}}) ∣_{0}^{1}$ $I = \underset{n = 1}{\sum^{\infty}} \frac{1}{n {(n + 1)}^{2}} [b y L^{'} H o p i t a l {r u l e}^{'} s]$ $I = \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + 1} - \frac{1}{{(n + 1)}^{2}})$ $t h e f i r s t s e r i e s \underset{n = 1}{\sum^{\infty}} (\frac{1}{n} - \frac{1}{n + 1}) i s$ $t e l e s c o p i n g \Rightarrow \lim_{p \to \infty} \underset{n = 1}{\sum^{p}} (\frac{1}{n} - \frac{1}{n + 1})$ $= \lim_{p \to \infty} (1 - \frac{1}{p + 1}) = 1$ $n o w t h e s e c o n d s e r i e s$ $\underset{n = 1}{\sum^{\infty}} \frac{1}{{(n + 1)}^{2}} = \underset{k = 2}{\sum^{\infty}} \frac{1}{k^{2}} = - 1 + \underset{k = 1}{\sum^{\infty}} \frac{1}{k^{2}}$ $= - 1 + \frac{π^{2}}{6} .$ $t h e r e f o r e I = \underset{0}{\int^{1}} \ln (x) \ln (1 - x) d x =$ $1 - (- 1 + \frac{π^{2}}{6}) = 2 - \frac{π^{2}}{6} . ★$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum