Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 117006 by TANMAY PANACEA last updated on 08/Oct/20

$${\int }_0^{100\pi }\mid sinx\mid dx$$

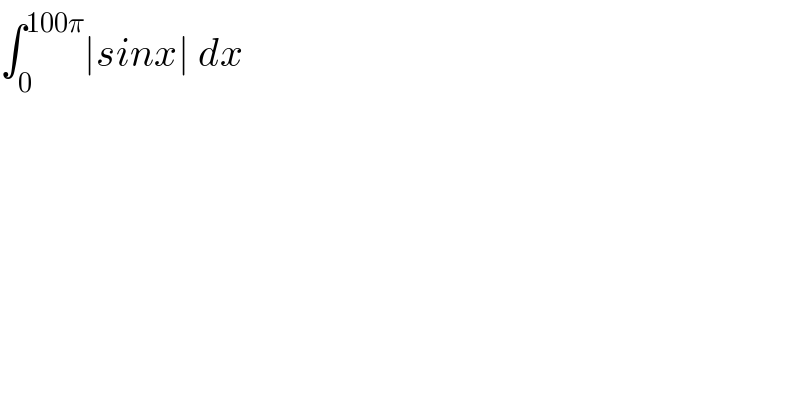
Commented by TANMAY PANACEA last updated on 08/Oct/20

$$thankyousir$$$$$$

Answered by mathmax by abdo last updated on 08/Oct/20

$$\mathrm{let}\mathrm{I}={\int }_0^{100\pi }\mid \mathrm{sinx}\mid \mathrm{dx}\Rightarrow \mathrm{I}=\sum _{\mathrm{k}=0}^{99}{\int }_{\mathrm{k}\pi }^{(\mathrm{k}+1)\pi }\mid \mathrm{sinx}\mid \mathrm{dx}$$$${=}_{\mathrm{x}=\mathrm{k}\pi +\mathrm{u}}\sum _{\mathrm{k}=0}^{99}{\int }_0^{\pi }\mid {(-1)}^{\mathrm{k}}\mathrm{sinu}\mid \mathrm{du}=\sum _{\mathrm{k}=0}^{99}{\int }_0^{\pi }\mathrm{sinu}\mathrm{du}$$$$=\sum _{\mathrm{k}=0}^{99}{[-\mathrm{cosu}]}_0^{\pi }=2\sum _{\mathrm{k}=0}^{99}\left(1\right)=2\times 100=200$$

Commented by TANMAY PANACEA last updated on 08/Oct/20

$$thankyousir$$

Commented by Bird last updated on 09/Oct/20

$$youarewelcomesir$$

Answered by TANMAY PANACEA last updated on 08/Oct/20

$$\mid sinx\mid graphisalaways+veandeachloopof$$$$sinxareais2.here100loopsoareais2\times 100=200$$$${\int }_0^{100\pi }\mid sinx\mid dx=100{\int }_0^{\pi }\mid sinx\mid dx=100\mid -cosx{\mid }_0^{\pi }$$$$=-100(-1-1)=200$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com